Let A be n×n matrix given by
A=⎡⎢
⎢
⎢
⎢
⎢⎣a11a12a13……a1na21a22a23…a2n⋮⋮⋮an1an2an3.ann⎤⎥
⎥
⎥
⎥
⎥⎦
Such that each horizontal row is arithmetic progression and each vertical column is a geometrical progression. It is known that each column in geometric progression have the same common ratio. Given that a24=1,a42=18 and a43=316
Let di be the common difference of the elements in with row then n∑i=1di is Solution in Punjabi
The correct Answer is:C
Step by step video & image solution for Let A be nxxn matrix given by A=[(a_(11),a_(12),a_(13)……a_(1n)),(a_(21),a_(22),a_(23)…a_(2n)),(vdots, vdots, vdots),(a_(n1),a_(n2),a_(n3).a_("nn"))] Such that each horizontal row is arithmetic progression and each vertical column is a geometrical progression. It is known that each column in geometric progression have the same common ratio. Given that a_(24)=1,a_(42)=1/8 and a_(43)=3/16 Let d_(i) be the common difference of the elements in with row then sum_(i=1)^(n)d_(i) is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LIMITSBOOK - ARIHANT MATHSCHAPTER - LIMITSEXERCISE - SOLVED EXAMPLES
1 Video
- LIMITSBOOK - ARIHANT MATHSCHAPTER - LIMITSEXERCISE - Exercise (Single Option Correct Type Questions)
38 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - ARIHANT MATHSCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
8 Videos
- LOGARITHM AND THEIR PROPERTIESBOOK - ARIHANT MATHSCHAPTER - LOGARITHM AND THEIR PROPERTIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
4 Videos
Similar Questions
To evaluate limx→a[f(x)], we must analyse the f(x) in right hand neighbourhood as well as in left hand neighbourhood of x=a. E.g. In case of continuous function, we may come across followign cases.
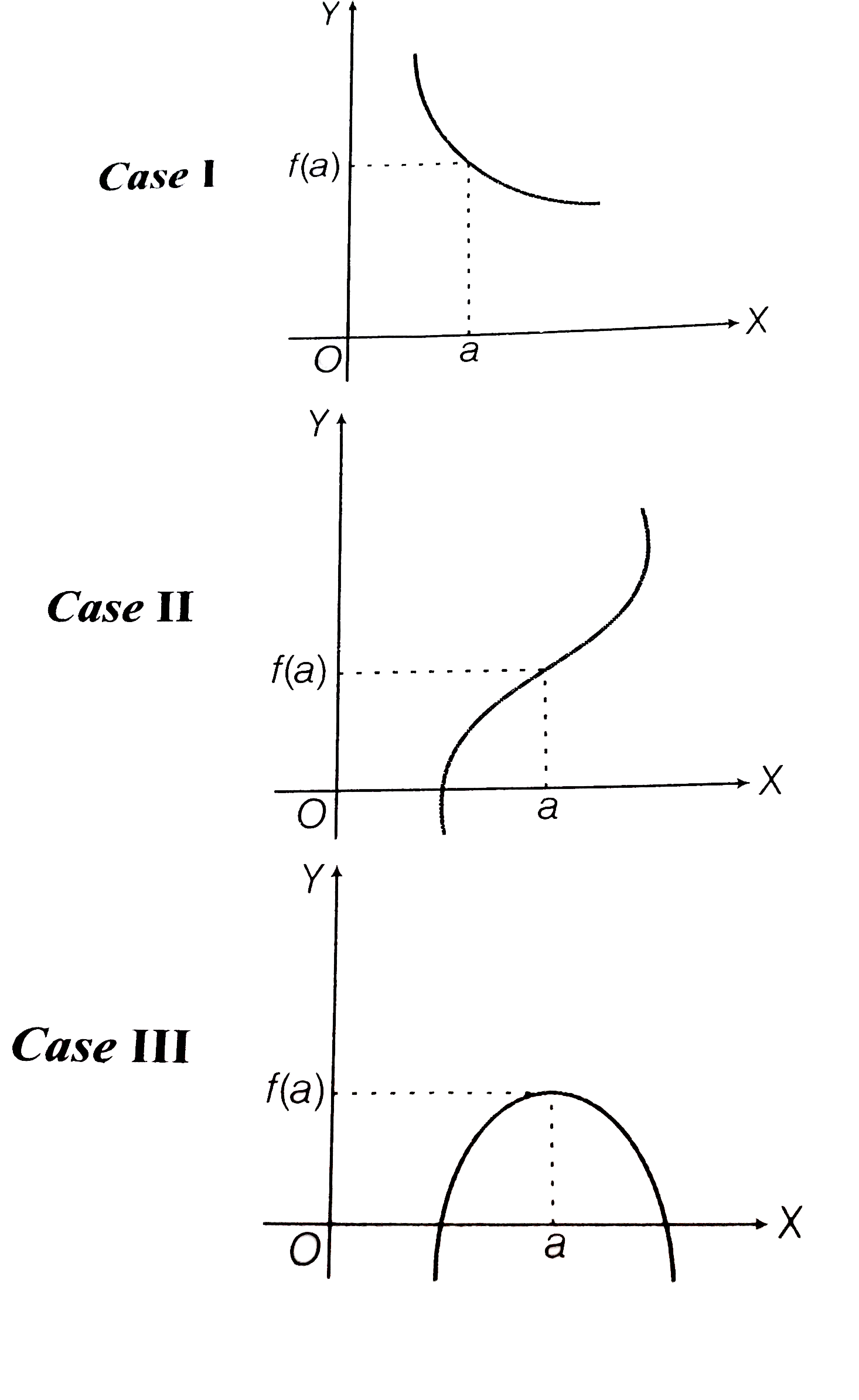

Iff(a) is an integer, the limit will exist in Case III and Case IV but not in Case I and Case II. If f(a) is not an integer, the limit exists in all the cases. ltbgt If f'(1)=−3 and limx→1[f(x)−12] does not exist, (where [.] denotes the greatest integer function), then
View Solutionlimx→0sin(πcos2(tan(sinx)))x2 is equal to
View SolutionIf α=3sin−1(611andβ=3cos−1(49), where the inverse trigonometric functions take only the principal values, then the correct options (s) is (are)
View SolutionIn Which quadrant Point (−2,−3) will be lie.
View SolutionIf Δ=∣∣ ∣∣a11a12a13a21a22a23a31a32a33∣∣ ∣∣ and Aij is cofactors of aij, then value of Δ is given by
View SolutionLet A be n×n matrix given by
A=⎡⎢ ⎢ ⎢ ⎢ ⎢⎣a11a12a13……a1na21a22a23…a2n⋮⋮⋮an1an2an3.ann⎤⎥ ⎥ ⎥ ⎥ ⎥⎦
Such that each horizontal row is arithmetic progression and each vertical column is a geometrical progression. It is known that each column in geometric progression have the same common ratio. Given that a24=1,a42=18 and a43=316
Let Sn=n∑j=1a4j,limn→∞Snn2 is equal to
View SolutionLet A be n×n matrix given by
A=⎡⎢ ⎢ ⎢ ⎢ ⎢⎣a11a12a13……a1na21a22a23…a2n⋮⋮⋮an1an2an3.ann⎤⎥ ⎥ ⎥ ⎥ ⎥⎦
Such that each horizontal row is arithmetic progression and each vertical column is a geometrical progression. It is known that each column in geometric progression have the same common ratio. Given that a24=1,a42=18 and a43=316
Let di be the common difference of the elements in with row then n∑i=1di is
View SolutionLet A be n×n matrix given by
A=⎡⎢ ⎢ ⎢ ⎢ ⎢⎣a11a12a13……a1na21a22a23…a2n⋮⋮⋮an1an2an3.ann⎤⎥ ⎥ ⎥ ⎥ ⎥⎦
Such that each horizontal row is arithmetic progression and each vertical column is a geometrical progression. It is known that each column in geometric progression have the same common ratio. Given that a24=1,a42=18 and a43=316
The value of limn→∞n∑i=1aii is equal to
View SolutionIf A=⎡⎢⎣a11a12a13a21a22a23a31a32a33⎤⎥⎦ and Aij denote the cofactor of element aij, then a11A21+a12A22+a13A23=
View SolutionIf A=⎡⎢⎣a11a12a13a21a22a23a31a32a33⎤⎥⎦andaij denote the cofactor of element Aij, then a11A11+a12A12+a13A13=
View SolutionIf a1,a2,a3,a4,a5 are consecutive terms of an arithmetic progression with common difference 3, then the value of ∣∣ ∣ ∣∣a23a2a1a24a3a2a25a4a3∣∣ ∣ ∣∣ is
View SolutionIf Δ=∣∣ ∣∣a11a12a13a21a22a23a31a32a33∣∣ ∣∣ and Aij is cofactors of aij, then value of Δ is given by
A. a11A31+a12A32+a13A33
B. a11A11+a12A21+a13A31
C. a21A11+a22A12+a23A13
D. a11A11+a21A21+a31A31
View SolutionFind minors and cofactors of the elements a11,a21in the determinant Δ=|a11a12a13a21a22a23a31a32a23|
View SolutionFind minors and cofactors of the elements a11,a21 in the determinant Δ=∣∣ ∣∣a11a12a13a21a22a23a31a32a33∣∣ ∣∣
View SolutionLet A be n×n matrix given by
A=⎡⎢ ⎢ ⎢ ⎢ ⎢⎣a11a12a13……a1na21a22a23…a2n⋮⋮⋮an1an2an3.ann⎤⎥ ⎥ ⎥ ⎥ ⎥⎦
Such that each horizontal row is arithmetic progression and each vertical column is a geometrical progression. It is known that each column in geometric progression have the same common ratio. Given that a24=1,a42=18 and a43=316
Let Sn=n∑j=1a4j,limn→∞Snn2 is equal to
View SolutionLet A be n×n matrix given by
A=⎡⎢ ⎢ ⎢ ⎢ ⎢⎣a11a12a13……a1na21a22a23…a2n⋮⋮⋮an1an2an3.ann⎤⎥ ⎥ ⎥ ⎥ ⎥⎦
Such that each horizontal row is arithmetic progression and each vertical column is a geometrical progression. It is known that each column in geometric progression have the same common ratio. Given that a24=1,a42=18 and a43=316
Let di be the common difference of the elements in with row then n∑i=1di is
View Solution