Let a ∈ R and f : R→R be given by f(x)=x5−5x+a, then
(a) f(x)=0 has three real roots if a>4
(b) f(x)=0 has only one real root if a>4
(c) f(x)=0 has three real roots if a<−4
(d) f(x)=0 has three real roots if −4<a<4
(a) f(x) has three real roots if a>4
(b) f(x) has only one real root if a>4
(c) f(x) has three real roots if a<−4
(d) f(x) has three real roots if −4<a<4
The correct Answer is:D
f(x)=x5−5x and g(x)=−a
∴f'(x)=5x4−5
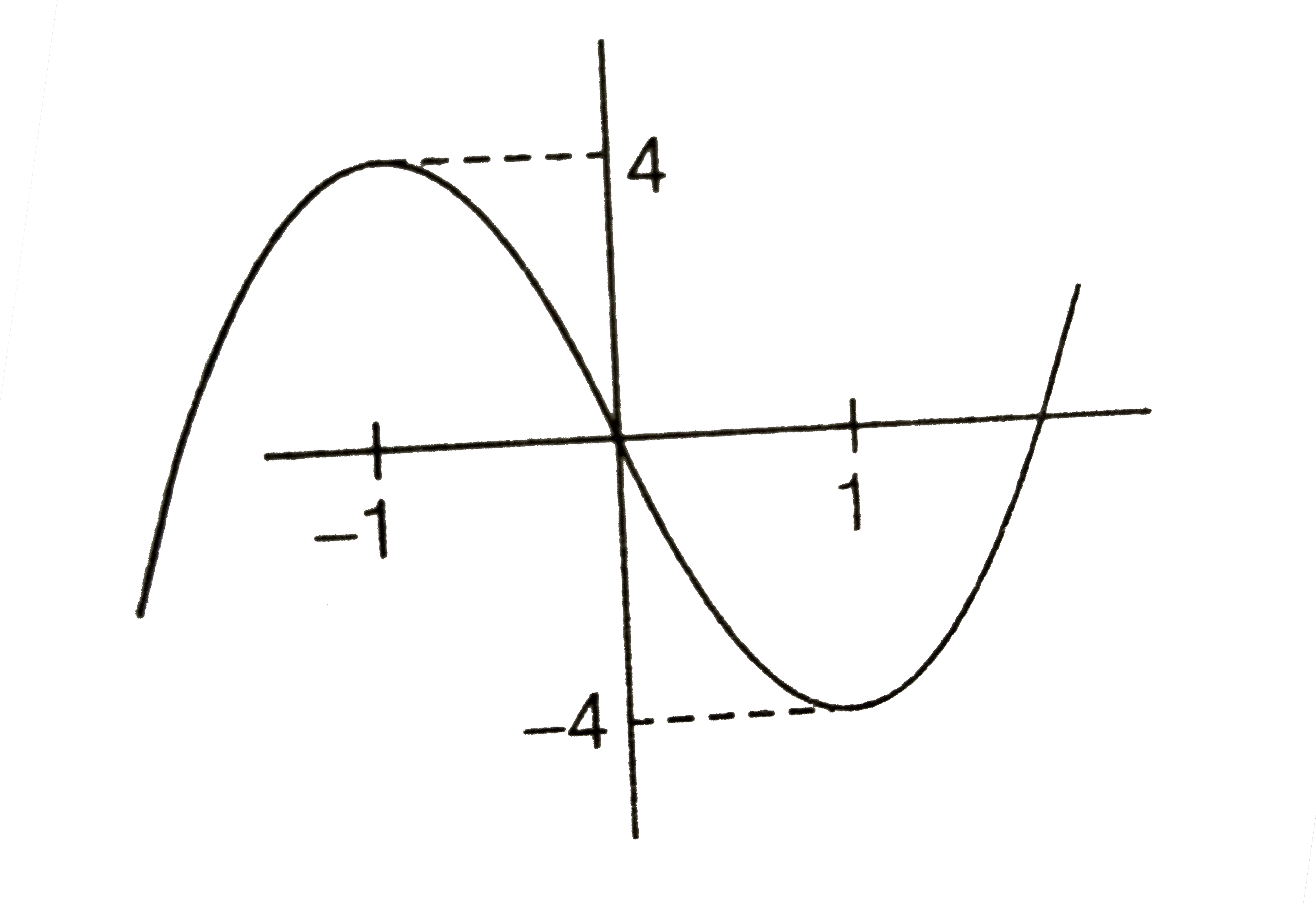
=5(x2+1)(x−1)(x+1)
Clearly f(x)=g() has one real root, if a>4 and three real roots if |a|<4.
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Subjective Type Questions)
24 Videos
- THE STRAIGHT LINESBOOK - ARIHANT MATHS ENGLISHCHAPTER - THE STRAIGHT LINESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
17 Videos
- THREE DIMENSIONAL COORDINATE SYSTEMBOOK - ARIHANT MATHS ENGLISHCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Three Dimensional Coordinate System Exercise 12 : Question Asked in Previous Years Exam
2 Videos
Similar Questions
Let a∈R and let f:R→ be given by f(x)=x5−5x+a, then (a) f(x) has three real roots if a>4 (b)f(x) has only one real roots if a>4 (c)f(x) has three real roots if a<−4 (d)f(x) has three real roots if −4<a<4
View SolutionIf the equaion x2+ax+b=0 has distinct real roots and x2+a|x|+b=0 has only one real root, then
View SolutionIf x2+bx+x=0 has no real roots and a+b+c<0 then
View SolutionFind the value of such that x3−|a|x2+3x+4=0 has only one real root.
View SolutionGiven that ax2+bx+c=0 has no real roots and a+b+c<0, then c≠0 b. c<0 c. c>0 d. c=0
View SolutionGiven that ax2+bx+c=0 has no real roots and a+b+c<0, then c≠0 b. c<0 c. c>0 d. c=0
View SolutionLet f(x)=3x−2+4x−3+5x−4. Then f(x)=0 has (A) exactly one real root in (2,3) (B) exactly one real root in (3,4) (C) at least one real root in (2,3) (D) none of these
View SolutionA particle is moving along x-direction with a constant acceleration a. The particle starts from x=x0 position with initial velocity u. We can define the position of the particle with time by the relation
x=x0+ut+12at2
plot the position of the particle in relation with time is following situations
(i) If initial position of the particle is on negativ x-axis, initial velocity is positive and acceleration is negative.
(ii) If initial position is positive, initial velocity is negative and acceleration is positive.
View SolutionIf the equation x3+px+q=0 has three real roots then show that 4p3+27q2<0.
View SolutionIf f(x)=ax2+bx+c,g(x)=−ax2+bx+c ,where ac≠0, then prove that f(x)g(x)=0 has at least two real roots.
View Solution
