Let A(1, 2), B(3, 4) be two points and C(x, y) be a point such that area of ΔABC is 3 sq. units and (x−1)(x−3)+(y−2)(y−4)=0. Then number of positions of C, in the xy plane is
2
4
8
none of these
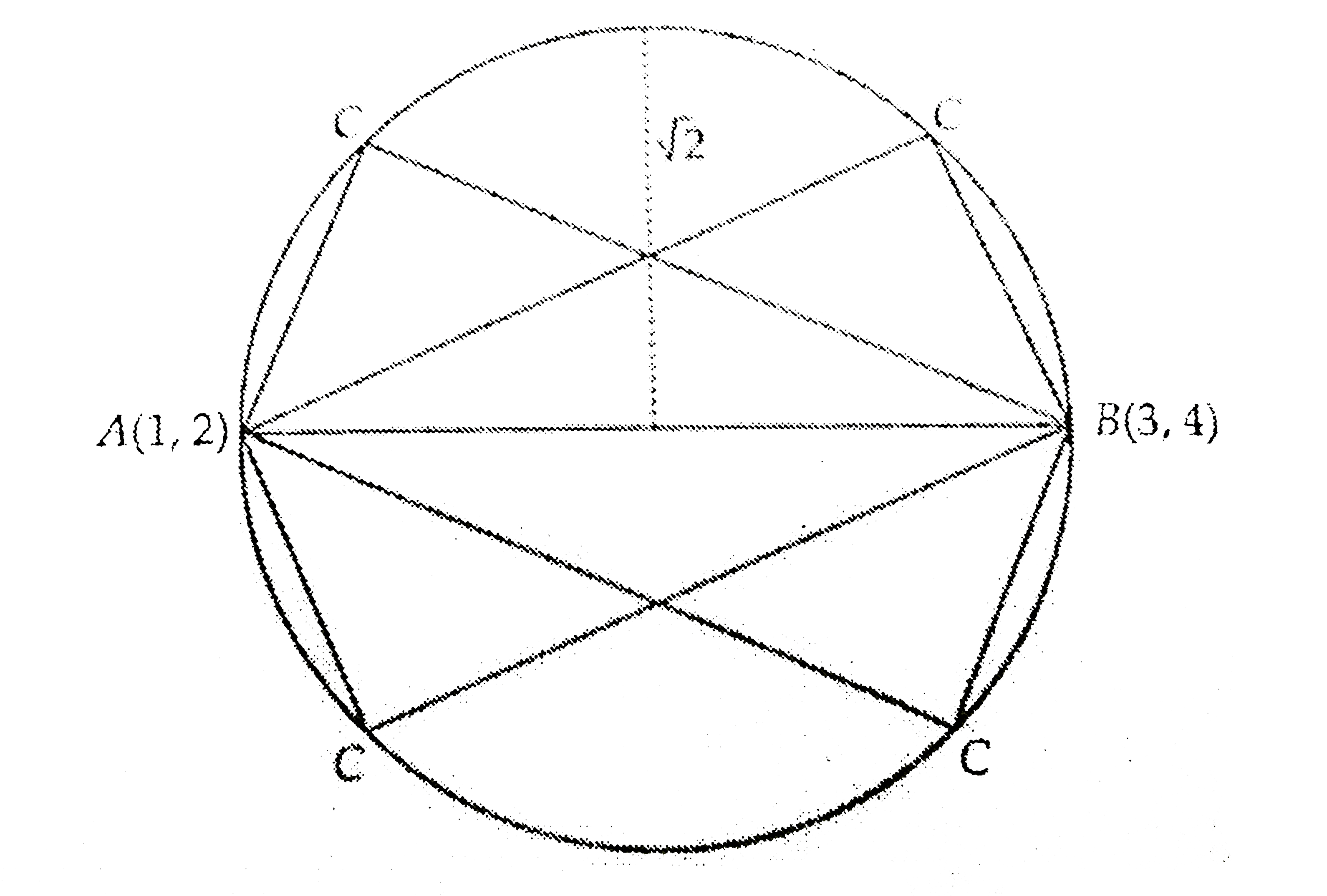
We have ,
(x - 1) (x-3) + (y-2) (y-4) = 0
⇒ Point C (x,y) lies on the circle with AB as a diameter .
Now ,
Area of ΔABC = 1 sq. unit
⇒12(AB)× (Altitude) = 1
⇒12×2√2× Altitude = 1 ⇒ Altitude = 1√2< Radius
Thus , there are four possible positions of C as shown in Fig. 35 .
Topper's Solved these Questions
- STRAIGHT LINESBOOK - OBJECTIVE RD SHARMACHAPTER - STRAIGHT LINESEXERCISE - Section-1 Solved MCQs (Example)
1 Videos
- STRAIGHT LINESBOOK - OBJECTIVE RD SHARMACHAPTER - STRAIGHT LINESEXERCISE - SECTION - II (ASSERTION - REASON TYPE MCQs)
14 Videos
- STRAIGHT LINESBOOK - OBJECTIVE RD SHARMACHAPTER - STRAIGHT LINESEXERCISE - ILLUSTRATION 18
1 Videos
- SETSBOOK - OBJECTIVE RD SHARMACHAPTER - SETSEXERCISE - Chapter Test
30 Videos
Similar Questions
Let A(1, 2), B(3, 4) be two points and C(x, y) be a point such that area of ΔABC is 3 sq. units and (x−1)(x−3)+(y−2)(y−4)=0. Then number of positions of C, in the xy plane is
View SolutionLet A(2,3),B(4,5) and let C=(x,y). be a point such that (x−2)(x−4)+(y−3)=0. If area of △ABC=√2 sq. unit, then maximum nunber of positions of C in the xy plane is
View Solution
Knowledge Check
Let A (2,3),B(4,5) be two points and let C=(x,y) be a point such that (x−2)(x−4)+(y−3)(y−5)=0 If area of ΔABC=√2aq. Units, then find the maximum number of positions of C in the xy plane.
A1B2C3D4Let A(1, 1, 1), B(3, 7, 4) and C (-1, 3, 0) be three
points in a plane.
Area of the triangle ABC is (in sq. units)A√2357114B√2038414C√2531214D√1432114The image of the point (−1,3,4) in the plane x−2y=0 is
A(15,11,4)B(−173,−193,1)C(8,4,4)D(95,−135,4)
Let A(1,1) and B(3,3) be two fixed points and P be a variable point such that area of ΔPAB remains constant and equal to 1 sq.units,for all positions of P ,then locus of P is given by
(A) 2y=2x+1 (B) 2y=2x-1 (C) y=x+1 (D) y=x-1
View SolutionLet P(2,-4) and Q(3,1) be two given points. Let R(x, y) be a point such that (x-2)(x-3)+(y-1)(y+4)=0 .If area of ΔPQR is 132 , then the number of possible positions of R are
View SolutionLet A=(1,2),B=(3,4)andC=(x,y) lie on the circumcircle of triangle ABC having AB as a diameter such that area of triangle ABC=1 the maximum number of position of C in the x-y plane is:
View Solutionthen image of the point (−1,3,4) in the plane x−2y=0
View SolutionThe image of the point (−1,3,4) in the plane x−2y=0 is
View Solution
