Let be two matrices. Consider the statements (i) and (ii) are false, (iii) is true (ii) and (iii) are false, (i) is true (i) is false (ii) and, (iii) are true (i) and (iii) are false, (ii) is true
(i) and (ii) are false, (iii) is true
(ii) and (iii) are false, (i) is true
(i) is false, (ii) and (iii) are true
(i) and (iii) are false, (ii) is true
The correct Answer is:D
(i) is false.
If and , then
(ii) is true as the product AB is an identity matrix, if and only if B is inverse of the matrix A.
(iii) is false since matrix multiplication in not commutative.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - MATRICESEXERCISE - Exercise (Multiple)33videos
MATRICES
- BOOK - CENGAGECHAPTER - MATRICESEXERCISE - Exercise (Comprehension)18videos
MATRICES
- BOOK - CENGAGECHAPTER - MATRICESEXERCISE - Exercise 13.517videos
MATRICES
- BOOK - CENGAGECHAPTER - MATHMETICAL REASONINGEXERCISE - JEE Previous Year10videos
MATHMETICAL REASONING
- BOOK - CENGAGECHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - Single Correct Answer Type46videos
METHODS OF DIFFERENTIATION
Similar Questions
Let AandB be two 2×2 matrices. Consider the statements (i) AB=O⇒A=OorB=O (ii)AB=I2⇒A=B−1 (iii) (A+B)2=A2+2AB+B2 (i) and (ii) are false, (iii) is true (ii) and (iii) are false, (i) is true (i) is false (ii) and, (iii) are true (i) and (iii) are false, (ii) is true
View SolutionThe factors of a2−2ab+b2 are (a+b)and(a+b). True or false.
View SolutionState whether the statements are true or falsea−b=b−a
View Solution(c−a) will be equal to 10(a+c) II. 10a+2b a. only I is true b. Only II is true c. Both I and II are true d. Both I and II are false
View SolutionState whether the statements are true or falsea÷(−b)=−(a÷b)
View SolutionLet A and B are two matrices then which of the following is always true? (i) A+B=B+A (ii)A+B=B−A (iii)A−B=B−A (iv) AB=BA
View SolutionState True or False: ab>ba is true. If a=3 and b=4, but false if a=2 and b=3.
View SolutionIn Figure, which of the following statements must be true? (i) a+b=d+c (ii) a+c+e=1800 (iii) b+f=c+e (a) (i) only (b) (ii) only (c) (iii) only (d) (ii) and (iii) only
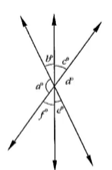 View Solution
View SolutionConsider the following two statements on power sharing and select the answer using the codes given below:
A. Power sharing is good for democracy
B. It helps to reduce the possibility of conflict between social groups.
Which of these statements are true and false?
(i) A is true but B is false
(ii) Both A and Bare true
(iii) Both A and Bare false
(iv) A is false but Bis trueView SolutionConsider the following statements concerning a ΔABc (i) The sides a,b,c and area of triangle are rational. (ii) a,tanB2,tanC2 are rational (iii) a,sinAsinB,sinC are rational . Prove that (i)⇒(ii)⇒(iii)⇒(i)
View Solution

