Let A,B, and C be three sets such that
A={(x,y)∣xcosθ=ysinθ=5,where'θ'is parameter}
B={(x,y)∣x−3cosϕ=y−4sinϕ=r}
C={(x,y)∣(x−3)2+(y−4)2≤R2}
If ϕ is fixed and r varies and (A∩B)=1, then secϕ is equal to
A
54
B
−54
C
53
D
−53
Text Solution
The correct Answer is:2
A={(x,y)}xcosθ=ysinθ=5, where θ is parameter }
A is set of points which lie of the circle C1:x2+y2=25
B={(x,y)∣x−3cosϕ=y−4sinϕ=r}
Ifϕ varies and r is fixed, then B is the set of all points which lie on a circle C2:(x−3)2+(y−4)2=r2
And if ϕ is fixed and r varies, then B is the set of all points which lie on the straight line L:y−4=tanθ(x−3).
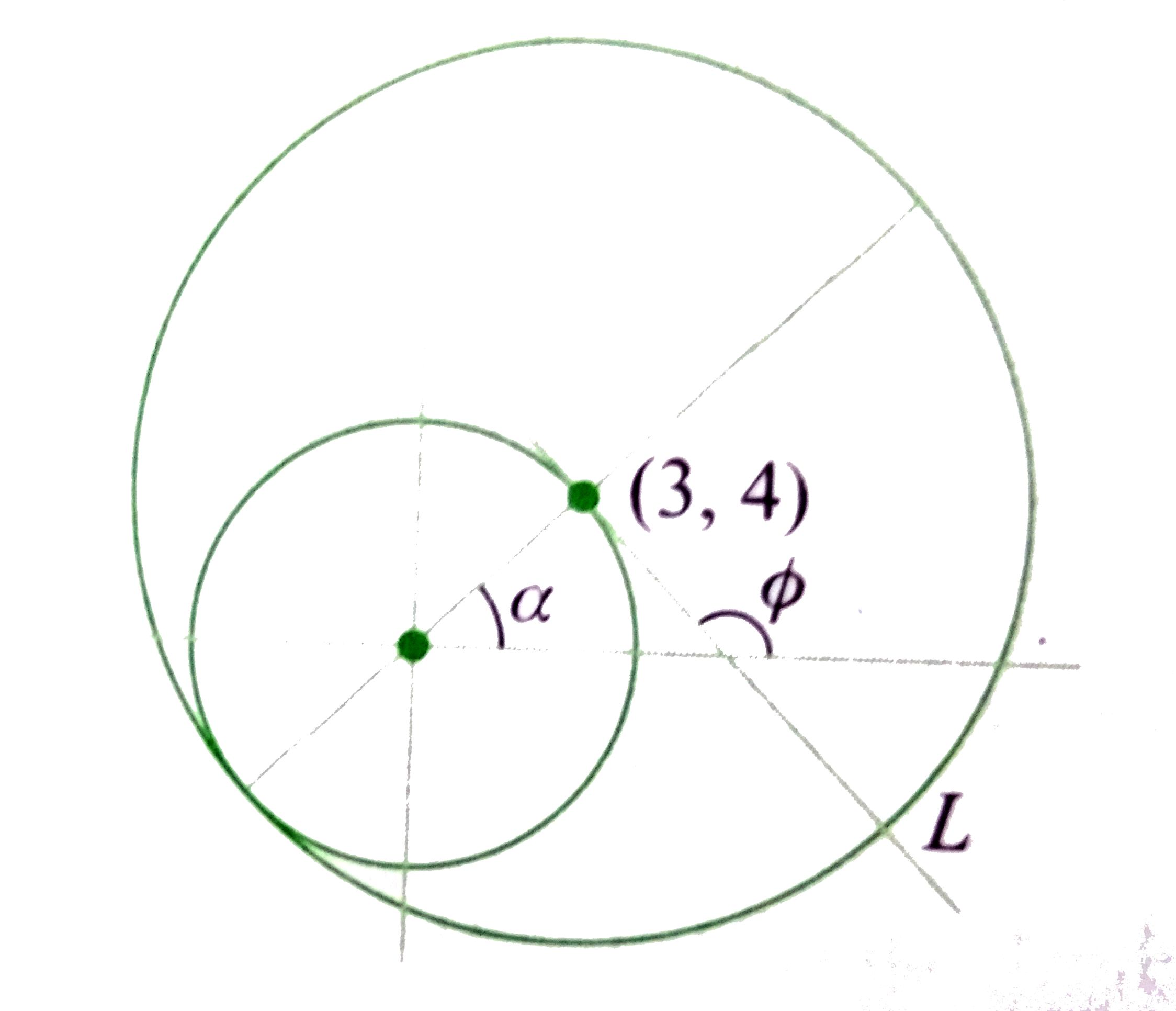
Now, if A∩C=A
Both circle C1 and C2 must touch each other internally.
So, R must be 10.
If ϕ is fixed and r varies and n(A∩B)=1, circle C1 touches line L.
ϕ=90∘+α
∴secϕ=sec(90∘+α)=−cosectα=−54
|
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - MATRIX MATCH TYPE
6 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Matrix)
1 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)
25 Videos
- BINOMIAL THEORMBOOK - CENGAGECHAPTER - BINOMIAL THEORMEXERCISE - Question Bank
31 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
Similar Questions
Knowledge Check
Let A,B, and C be three sets such that
A={(x,y)∣xcosθ=ysinθ=5,where'θ'is parameter}
B={(x,y)∣x−3cosϕ=y−4sinϕ=r}
C={(x,y)∣(x−3)2+(y−4)2≤R2}
If A∩C=A, then minimum value of R isA5B6C10D11If x=cosθ+isinθ,y=cosϕ+isinϕz=cosΨ+isinΨandyz+zx+xy=1 then
cos(ϕ−Ψ)+cos(Ψ−θ)+cos(θ−ϕ) is equal toA3/2B−3/2C0D1
If ysinϕ=xsin(2θ+ϕ) show that (x+y)cot(θ+ϕ)=(y−x)cotθ.
View SolutionIf 2cosθ=x+1x and 2cosϕ=y+1y, then
View SolutionIf ydydx=x⎡⎢ ⎢ ⎢ ⎢⎣y2x2+ϕ(y2x2)ϕ'(y2x2)⎤⎥ ⎥ ⎥ ⎥⎦,x≥0,ϕ>0, y(1) = -1, then ϕ(y24) is equal to :
View SolutionLet dydx=yϕ'(x)−y2ϕ(x), where ϕ(x) is a specified function satisfying ϕ(1)=1,ϕ(2)=130. If y(1)=1 then y(2) is equal to
View SolutionLet dydx=yϕ'(x)−y2ϕ(x), where ϕ(x) is a function satisfies ϕ(1)=1,ϕ(4)=1296. If y(1) = 1 then y(4) is equal to__________
View SolutionLet dydx=yϕ'(x)−y2ϕ(x), where ϕ(x) is a function satisfies ϕ(1)=1,ϕ(4)=1296. If y(1) = 1 then y(4) is equal to__________
View Solution
