Let ABC be a triangle and M be a point on side AC closer to vertex C than A. Let N be a point on side AB such that MN is parallel to BC and let P be a point on side BC such that MP is parallel to AB. If the area of the quadrilateral BNMP is equal to th of the area of triangle ABC, then the ratio AM/MC equals.
5
6
The correct Answer is:A

To find ..(i)
Put in (iii)
Not true as M is near to C than A
Topper's Solved these Questions
Similar Questions
In triangle ABC, angle B is obtuse. D and E are mid-points of sides AB and BC respectively and F is a point on side AC such that EF is parallel to AB. Show that BEFD is a parallelogram.
View SolutionLet P, Q, R be the mid-points of sides AB, BC, CA respectively of a triangle ABC. If the area of the triangle ABC is 5 square units, then the area of the triangle PQR is
View Solution
Knowledge Check
D and E are points on sides AB and AC of ΔABC. DE is parallel to BC. If AD : DB = 2 : 3, what is the ratio of area ΔADE and area of quadrilateral BDEC ?
A4:21B4:25C4:29D4:9If D, E and F are the mid-points of sides BC, CA and AB respectively of △ABC, then the ratio of the areas of △DEF to the area of △ABC is :
A1:4B1:2C1:3D2:3Points P and Q lie on sides AB and AC of triangle ABC respectively such that segment PQ is parallel to side BC. If the ratio of areas of triangle APQ: triangle ABC is 25 : 36, then the ratio PA : PB is
A5:6B1:5C6:5D5:1
If D is a point on the side AB of ΔABC such that AD:BD=3:2andE is a point on BC such that DE∣∣AC, find the ratio of the areas of ΔABCandΔDBE
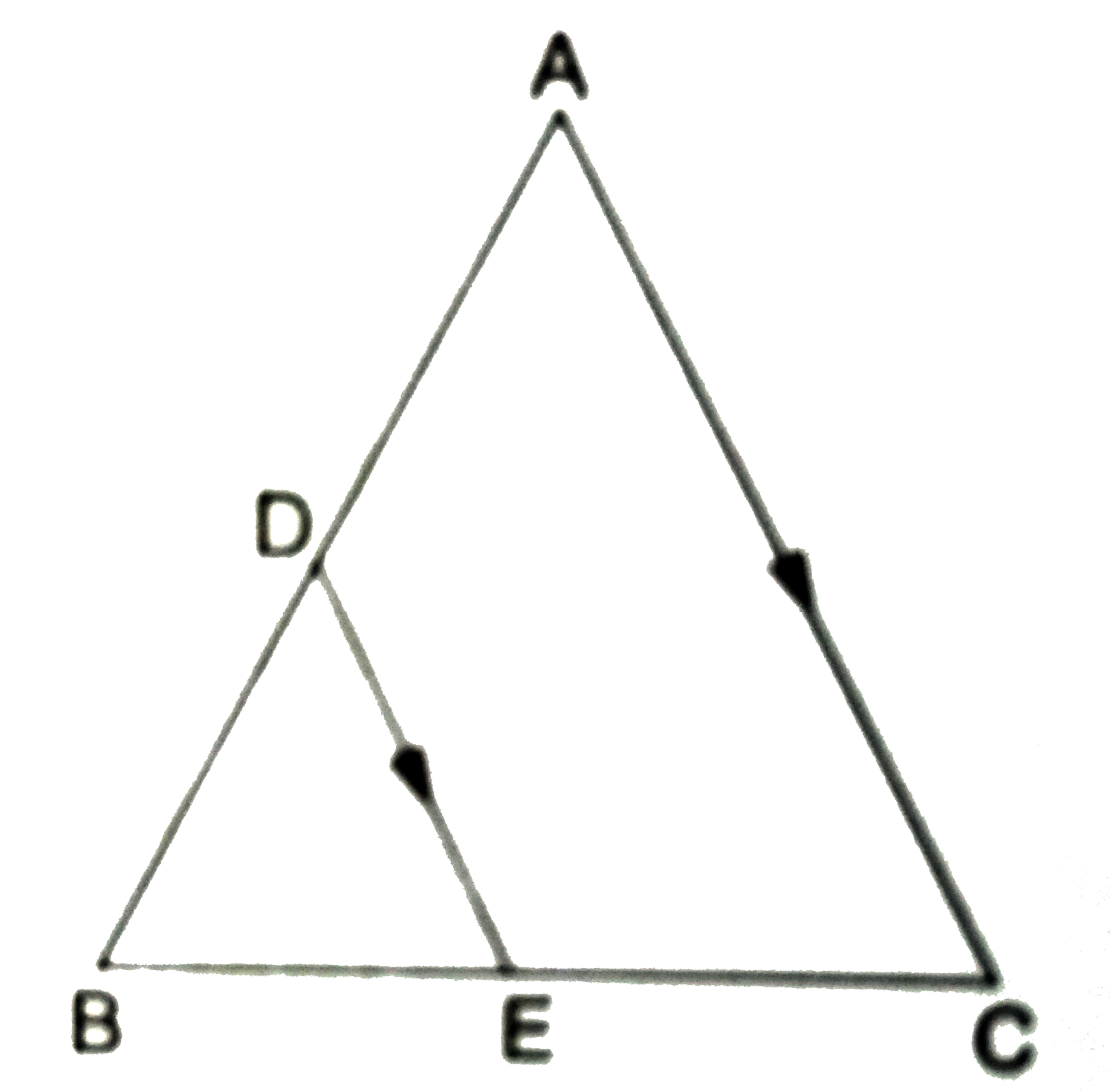
View SolutionABC is a triangle right angled at B. Let M and N be two points on AB such that AM = MN = NB. Let P and Q be two points on AC such that PM is parallel to QN and QN is parallel to CB. If BC= 12 cm, then what is (PM + QN) equal to?
View SolutionIn triangle ABC, D and E are mid-points of sides AB and BC respectively. Also, F is a point in side AC so that DF is parallel to BC
(i) Prove that DBEF is a parallelogram.
View SolutionSuppose ABC is a triangle with AB of unit length. D and E are the points lying on AB and AC respectively such that BC and DE are parallel. If the area of triangle ABC is twice the area of triangle ADE, then the length of AD is
View SolutionIn triangle ABC, AB>AC and D is a point in side BC. Show that : AB>AD.
View Solution
