Let ABC be a triangle with incentre I. If P and Q are the feet of the perpendiculars from A to BI and CI, respectively, then prove that APBI+AQCl=cot.A2
To prove that APBI+AQCI=cotA2, we can follow these steps:
Step 1: Understand the Geometry
Let ABC be a triangle with incenter I. Points P and Q are the feet of the perpendiculars from A to BI and CI, respectively.
Step 2: Use Triangle Properties
In triangle APB, since P is the foot of the perpendicular from A to BI, we have:
sinB2=APAB
Thus, we can express AP as:
AP=AB⋅sinB2
Step 3: Apply Sine Rule in Triangle ABI
Using the sine rule in triangle ABI:
BIsinA2=ABsin(90∘−B2)=ABcosB2
From this, we can express BI as:
BI=AB⋅sinA2cosB2
Step 4: Find APBI
Now substituting AP and BI into APBI:
APBI=AB⋅sinB2AB⋅sinA2cosB2=sinB2⋅cosB2sinA2=12sinBsinA2
Step 5: Repeat for AQ
In triangle AQC, using similar reasoning:
AQ=AC⋅sinC2
And using the sine rule in triangle ACI:
CIsinA2=ACcosC2
So, we can express CI as:
CI=AC⋅sinA2cosC2
Thus, we find AQCI:
AQCI=AC⋅sinC2AC⋅sinA2cosC2=sinC2⋅cosC2sinA2=12sinCsinA2
Step 6: Combine the Results
Now we can combine the results:
APBI+AQCI=12sinBsinA2+12sinCsinA2=12⋅sinB+sinCsinA2
Step 7: Use the Sine Addition Formula
Using the sine addition formula:
sinB+sinC=2sin(B+C2)cos(B−C2)
Since B+C=180∘−A, we have:
sinB+sinC=2sin(90∘−A2)cos(B−C2)=2cosA2cos(B−C2)
Step 8: Final Expression
Thus, we can write:
APBI+AQCI=12⋅2cosA2cos(B−C2)sinA2=cosA2cos(B−C2)sinA2
This simplifies to:
cotA22
Thus, we have:
APBI+AQCI=cotA2
Let ABC be a triangle with incenter I. Points P and Q are the feet of the perpendiculars from A to BI and CI, respectively.
In triangle APB, since P is the foot of the perpendicular from A to BI, we have:
sinB2=APAB
Thus, we can express AP as:
AP=AB⋅sinB2
Using the sine rule in triangle ABI:
BIsinA2=ABsin(90∘−B2)=ABcosB2
From this, we can express BI as:
BI=AB⋅sinA2cosB2
Now substituting AP and BI into APBI:
APBI=AB⋅sinB2AB⋅sinA2cosB2=sinB2⋅cosB2sinA2=12sinBsinA2
In triangle AQC, using similar reasoning:
AQ=AC⋅sinC2
And using the sine rule in triangle ACI:
CIsinA2=ACcosC2
So, we can express CI as:
CI=AC⋅sinA2cosC2
Thus, we find AQCI:
AQCI=AC⋅sinC2AC⋅sinA2cosC2=sinC2⋅cosC2sinA2=12sinCsinA2
Now we can combine the results:
APBI+AQCI=12sinBsinA2+12sinCsinA2=12⋅sinB+sinCsinA2
Using the sine addition formula:
sinB+sinC=2sin(B+C2)cos(B−C2)
Since B+C=180∘−A, we have:
sinB+sinC=2sin(90∘−A2)cos(B−C2)=2cosA2cos(B−C2)
Thus, we can write:
APBI+AQCI=12⋅2cosA2cos(B−C2)sinA2=cosA2cos(B−C2)sinA2
This simplifies to:
cotA22
Thus, we have:
APBI+AQCI=cotA2
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Illustration86videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.112videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )1videos
PROGRESSION AND SERIES
- BOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Archives(Matrix Match Type)1videos
RELATIONS AND FUNCTIONS
Similar Questions
Let ABC be a triangle with incentre at I Also, let P and Q be the feet of perpendiculars from A to BI and CI respectively. Then which of the following results are correct? APBI=sinB2cosC2sinA2 (b) AQCI=sinC2cosB2sinA2 APBI=sinC2cosB2sinA2 (d) APBI+AQCI=√3if∠A=600
View SolutionLet ABC be a triangle with incentre I and inradius r. Let D, E, F be the feet of the perpendiculars from I to the sides BC, CA and AB, respectively, If r2 and r3 are the radii of circles inscribed in the quadrilaterls AFIE, BDIF and CEID respectively, then prove that r1r−r1+r2r−r2+r3r−r3=r1r2r3(r−r1)(r−r2)(r−r3)
View SolutionLet ABC be an acute angled triangle with orthocenter H.D, E, and F are the feet of perpendicular from A,B, and C, respectively, on opposite sides. Also, let R be the circumradius of ΔABC. Given AH.BH.CH=3and(AH)2+(BH)2+(CH)2=7
Then answer the following
Value of R isView SolutionFor a triangle ABC,R=52andr=1. Let D, E and F be the feet of the perpendiculars from incentre I to BC, CA and AB, respectively. Then the value of (IA)(IB)(IC)(ID)(IE)(IF) is equal to _____
View SolutionFor triangle ABC,R=52andr=1. Let I be the incenter of the triangle and D,EandF be the feet of the perpendiculars from I→BC,CAandAB, respectively. The value of ID⋅IE⋅IFIA⋅IB⋅IC is equal to (a) 52 (b) 54 (c) 110 (d) 15
View SolutionLet f,gandh be the lengths of the perpendiculars from the circumcenter of ΔABC on the sides a, b, and c, respectively. Prove that af+bg+ch=14abcfgh
View SolutionLet ABC be a triangle having O and I as its circumcentre and incentre, respectively. If R and r are the circumradius and the inradius respectively, then prove that (IO) 2 =R 2 −2Rr. Further show that the triangle BIO is right angled triangle if and only if b is the arithmetic mean of a and c.
View SolutionIf x,yandz are the distances of incenter from the vertices of the triangle ABC , respectively, then prove that abcxyz=cot(A2)cot(B2)cot(C2)
View SolutionIn the given figure ABC is a triangle and D is the mid-point of BC. AD is produced to E. BM and CN are two perpendiculars dropped from B and C respectively on AE.
Prove that : (i) ΔBMD≅ΔCND (ii) BM = CN
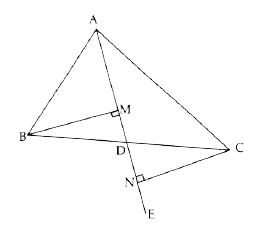 View Solution
View SolutionIf the mid-points P, Q and R of the sides of the ΔABC are (3,3),(3,4)and(2,4) respectively, then ΔABC is
View Solution

