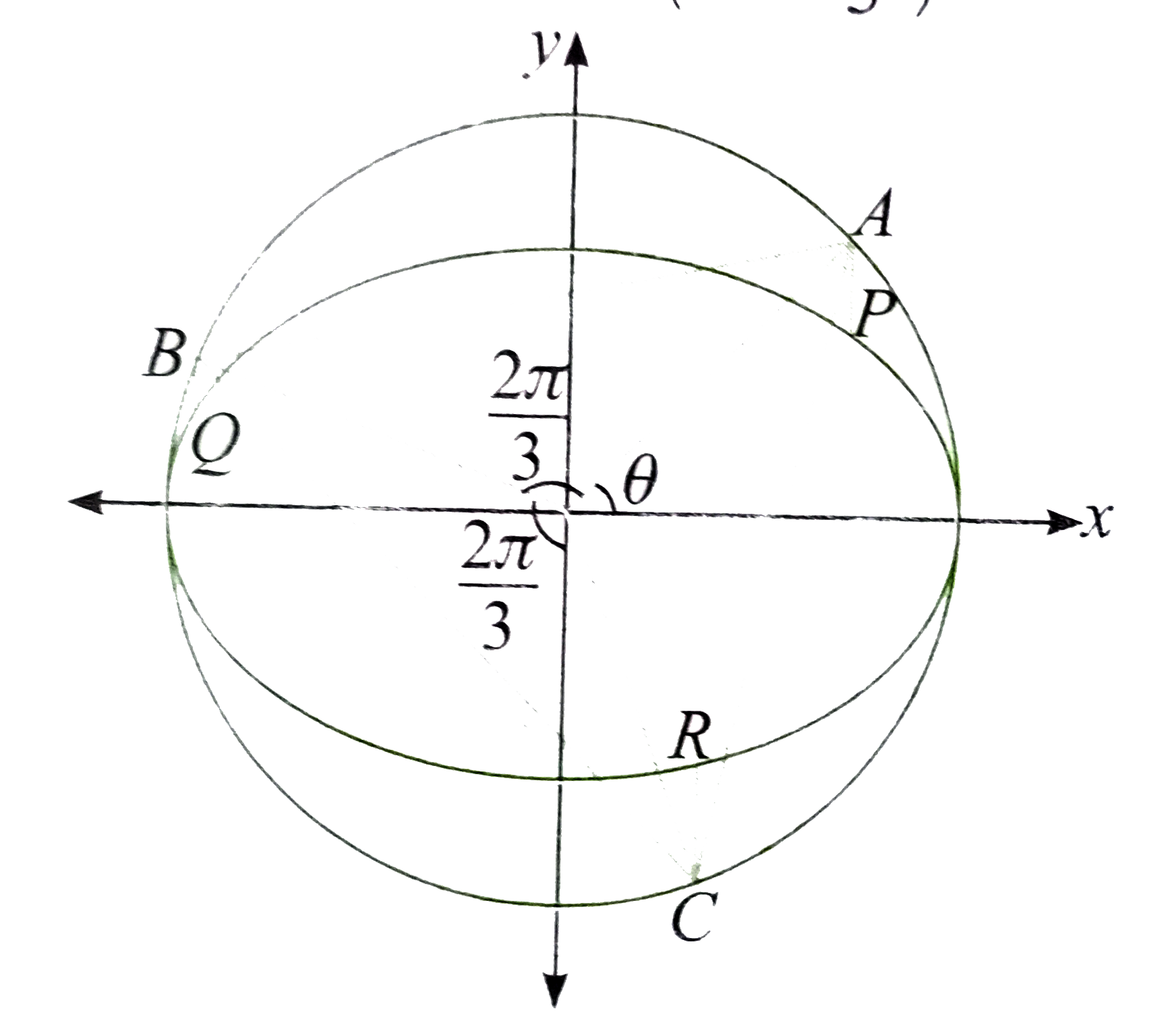
Let ABC be an equilateral triangle inscribed in the circle $x^{2} + y^{2} = a^{2}$ . Suppose pendiculars from A, B, C to the ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1, (a > b)$ meets the ellipse respectivelily at P, Q, R so that P, Q , R lies on same side of major axis as A, B, C respectively. Prove that the normals to the ellipse drawn at the points P Q nad R are concurrent. Solution in Tamil

Video Solution

Text Solution

Verified by Experts

Let A , B and C, be the points on the cicle whose cooridnates are
$A (a cos θ, a sin θ)$
$B (a cos (θ + \frac{2 π}{3}), a sin (θ + \frac{2 π}{3}))$
$C (a cos (θ + \frac{4 π}{3}), a sin (θ + \frac{4 π}{3}))$
Hence, $P \equiv (a cos θ, b sin θ)$
$Q \equiv (a cos (θ + \frac{2 π}{3}), a sin (θ + \frac{2 π}{3}))$
$R \equiv (a cos (θ + \frac{4 π}{3}), a sin (θ + \frac{4 π}{3}))$
It is given that P,Q and R are on the same side of the x-axis as A,B, and C.
So, the required nomrmals ot the ellipse at P,Q and R are
$a x sec θ - by cosec θ = a^{2} - b^{2} (1)$
$a x sec (θ + \frac{2 π}{3} - by cosec (θ + \frac{2 π}{3}) = a^{2} - n^{2} (2)$
$a x sec (θ + \frac{4 π}{3} - by cosec (θ + \frac{4 π}{3}) = a^{2} - n^{2} (3)$

Now, $Δ$ = $∣ ∣ ∣ ∣ ∣ ∣ \begin{matrix} sec θ & cosec θ & 1 sec (θ + \frac{2 π}{3}) & cosec (θ + \frac{2 π}{3}) & 1 sec (θ + \frac{2 π}{3}) & cosec (θ + \frac{2 π}{3}) & 1 \end{matrix} ∣ ∣ ∣ ∣ ∣ ∣$
Multiplying $R_{1}, R_{2} and R_{3}$ , by $sin θ cos, θ, sin (θ + \frac{2 π}{3}) c o (θ + \frac{2 π}{3}) and sin (θ + \frac{4 π}{3})$ respectively, we get
$Δ = \frac{1}{k} ∣ ∣ ∣ ∣ ∣ ∣ \begin{matrix} sin θ & cos θ & sin 2 θ sin (θ + \frac{2 π}{3}) & cos (θ + \frac{2 π}{3}) & sin (2 θ + \frac{4 π}{3}) sin (θ - \frac{2 π}{3}) & cos (θ - \frac{2 π}{3}) & sin (2 θ - \frac{4 π}{3}) \end{matrix} ∣ ∣ ∣ ∣ ∣ ∣$
Where
$k = 2 sin θ cos θ sin (θ + \frac{2 π}{3}) cos (θ - \frac{2 π}{3}) sin (θ + \frac{4 π}{3}) cos (θ + \frac{4 π}{3})$
Operating $R_{2} \to R_{2} + R_{3}$
$Δ = \frac{1}{k} ∣ ∣ ∣ ∣ ∣ ∣ \begin{matrix} sin θ & cos θ & sin 2 θ 2 sin θ \cdot cos . \frac{2 π}{3} & 2 cos θ \cdot cos . \frac{2 π}{3} & 2 sin θ \cdot cos . \frac{4 π}{3} sin (θ - \frac{2 π}{3}) & cos (θ - \frac{2 π}{3}) & sin (2 θ - \frac{4 π}{3}) \end{matrix} ∣ ∣ ∣ ∣ ∣ ∣$
$= \frac{1}{k} ∣ ∣ ∣ ∣ ∣ \begin{matrix} sin θ & cos θ & sin 2 θ - sin θ & - cos θ & - sin θ sin (θ - \frac{2 π}{3}) & cos (θ - \frac{2 π}{3}) & sin (2 θ - \frac{4 π}{3}) \end{matrix} ∣ ∣ ∣ ∣ ∣$

Updated on:21/07/2023

|

Class 12 MATHS QUESTION BANK

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile