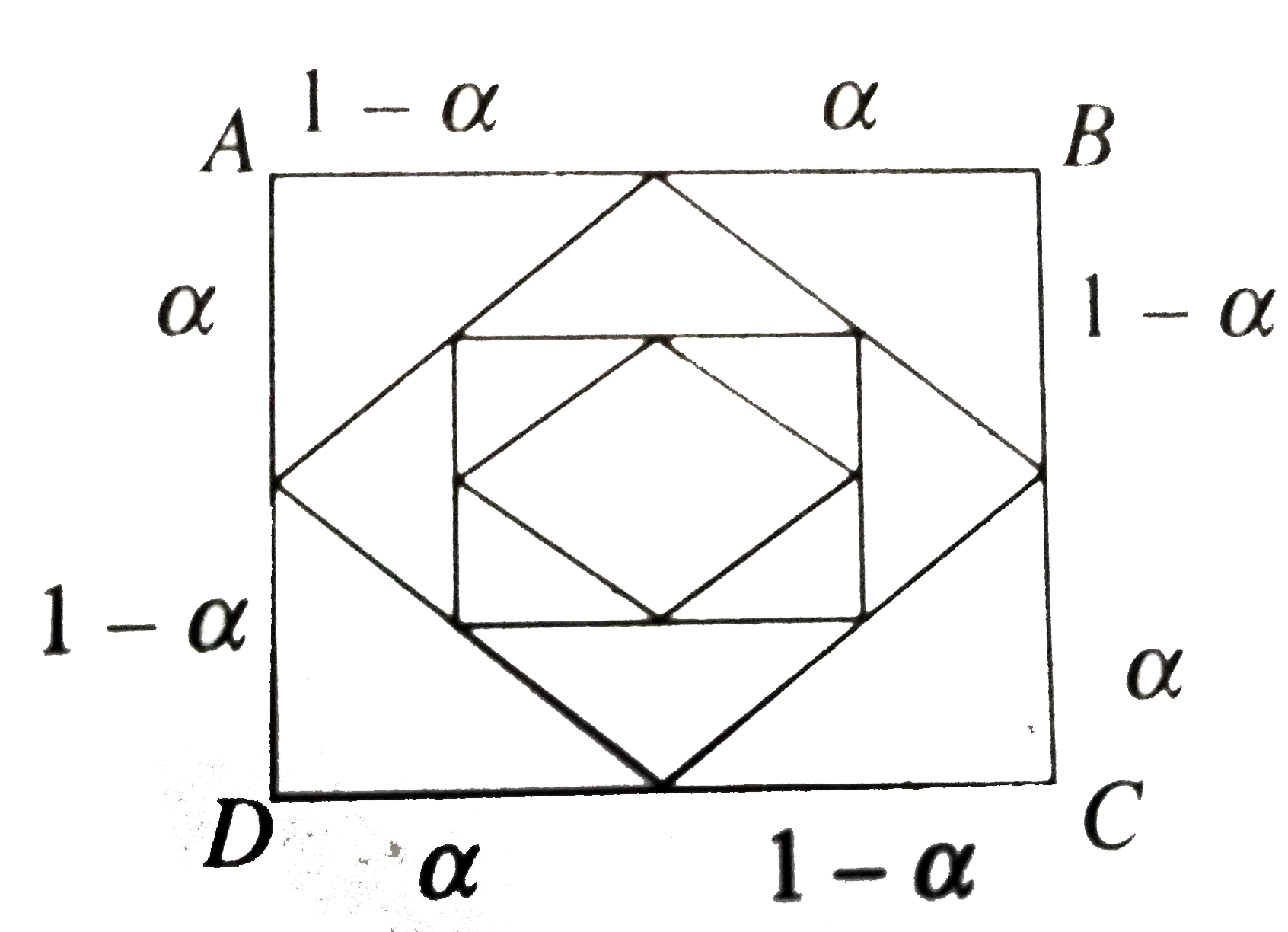
Let ABCD is a unit square and each side of the square is divided in the ratio α:(1−α)(0<α<1) . These points are connected to obtain another square. The sides of new square are divided in the ratio α:(1−α) and points are joined to obtain another square. The process is continued idefinitely. Let an denote the length of side and An the area of the nth square
Ifα=13, then the least value of n for which An>110 is
4
5
6
7
The correct Answer is:B
(b) 
Clearly from the diagram,
a1=1
(an+1)2=[(1−α)2+α2](an)2⇒An+1=[2α2−2α+1]An
For α=13, (an+1)2=59(an)2
⇒An+1An=59
⇒A2=59, A3=(59)2,...
⇒An=(59)n−1
An<110⇒(59)n−1<110
⇒ Least value of n is 5.
∞∑n=1An=83
⇒11−(2α2−2α+1)=83
⇒16α2−16α+3=0
⇒16α2−12α−4α+3=0
⇒(4α−1)(4α−3)=0
⇒α=14, 34
The side of nth square equal to the diagonal of (n+1)th square. ⇒√2an=an+1
⇒(an+1)2(an)2=12
⇒4α2−4α+1=0
⇒α=1/2
Topper's Solved these Questions
- PROGRESSION AND SERIESBook:CENGAGEChapter:PROGRESSION AND SERIESExercise:Multiple Correct Answer
Explore 4 Videos
- PROGRESSION AND SERIESBook:CENGAGEChapter:PROGRESSION AND SERIESExercise:Single correct Answer
Explore 54 Videos
- PROBABILITY IIBook:CENGAGEChapter:PROBABILITY IIExercise:NUMARICAL VALUE TYPE
Explore 2 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGEChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:JEE Advanced Previous Year
Explore 11 Videos
Similar Questions
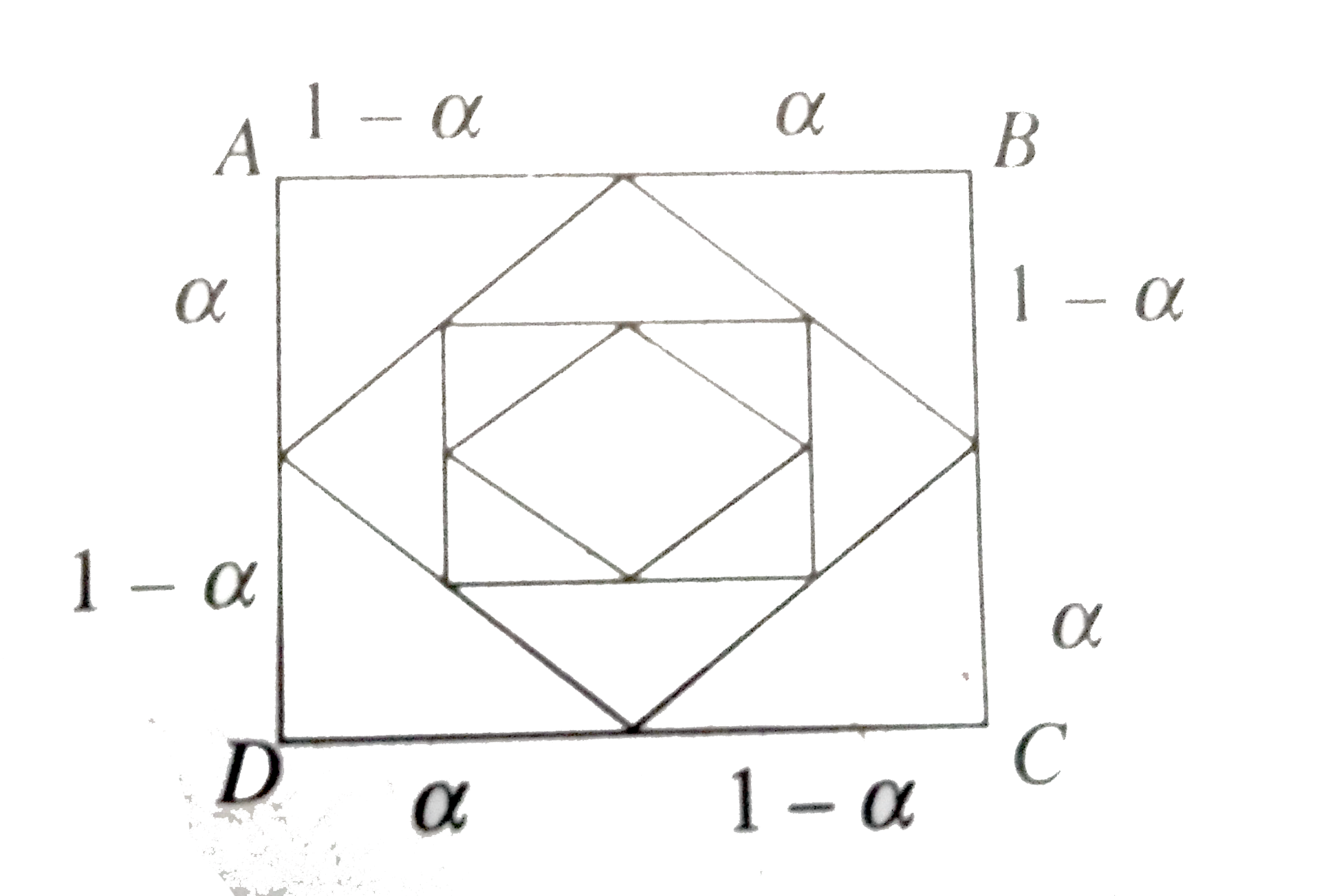
Let ABCD is a unit square and each side of the square is divided in the ratio α:(1−α)(0<α<1) . These points are connected to obtain another square. The sides of new square are divided in the ratio α:(1−α) and points are joined to obtain another square. The process is continued idefinitely. Let an denote the length of side and An the area of the nth square
The value of α for which ∞∑n=1An=83 is/are
View Solution Let ABCD is a unit square and each side of the square is divided in the ratio α:(1−α)(0<α<1) . These points are connected to obtain another square. The sides of new square are divided in the ratio α:(1−α) and points are joined to obtain another square. The process is continued idefinitely. Let an denote the length of side and An the area of the nth square
Let ABCD is a unit square and each side of the square is divided in the ratio α:(1−α)(0<α<1) . These points are connected to obtain another square. The sides of new square are divided in the ratio α:(1−α) and points are joined to obtain another square. The process is continued idefinitely. Let an denote the length of side and An the area of the nth square
The value of α for which side of nth square equal to the diagonal of (n+1)th square is
View Solution
Knowledge Check
The sides of the triangle are sinα , cosα and √1+sinαcosα for some 0<α<π2. Then the greatest angle of the triangle is
A150∘B90∘C120∘D60∘A square is drawn by joining mid-points of the sides of a square. Another square is drawn inside the second square in the same way and the process is continued indefinitely. If the side of the first square is 16 cm, then what is the sum of the areas of all the squares ?
(a)256sq. Cm
(b)512 sq. cm
(c)1024sq. Cm
(d)512/3sq. CmA256sq. CmB512 sq. cmC1024sq. CmD512/3sq. CmA square is drawn by joining mid pint of the sides of a square. Another square is drawn inside the second square in the same way and the process is continued in definitely. If the side of the first square is 16 cm, then what is the sum of the areas of all the squares ?
A256 sq cmB512 sq cmC1024 sq cmD512/3 sq cm
The side of a given square is 10 cm. The midpoints of its sides are joined to form a new square. Again, the midpoints of the sides of this new aquare are joined to form another square. The process is continued indefinitely. Find (i) the sum of the areas and (ii) the sum of the perimeters of the squares.
View SolutionThe side of a given square is equal to a. The mid-points of its sides are joined to form a new square. Again, the mid-points of the sides of this new square are joined to form another square. This process is continued indefinitely. Find the sum of the areas of the squares and the sum of the perimeters of the squares.
View Solution______ squares of each side 1 m makes a square of side 5 km.
View SolutionOne side of a square is inclined to the x-axis at an angle α and one of its extremities is at the origin. If the side of the square is 4, find the equations of the diagonals of the square.
View SolutionThe sides of the triangle are sinα , cosα and √1+sinαcosα for some 0<α<π2. Then the greatest angle of the triangle is
View Solution
