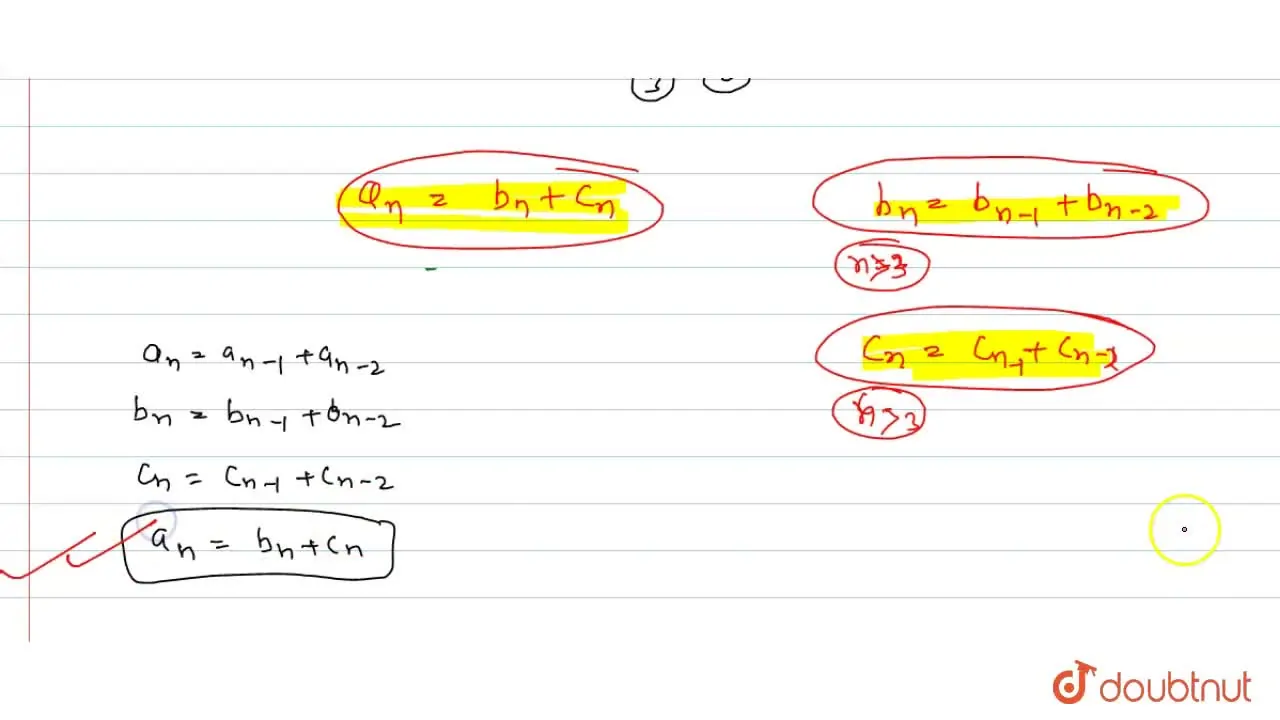
Let an denote the number of all n-digit numbers formed by the digits 0,1 or both such that no consecutive digits in them are 0. Let bn be the number of such n-digit integers ending with digit 1 and let cn be the number of such n-digit integers ending with digit 0. Which of the following is correct ?
7
8
9
11
The correct Answer is:B
Clearly,
an=bn+cn,bn=an−1 and cn=an−2
∴an=an−1+an−2
Also, a1=1,a2=2
∴a3=2+1=3,a4=a3+a2=3+2=5,
a5=a4+a3=5+3=8
∴b6=a5=8
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - MISCELLANEOUS EQUATIONS AND INEQUATIONS EXERCISE - Exercise30videos
MISCELLANEOUS EQUATIONS AND INEQUATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - MISCELLANEOUS EQUATIONS AND INEQUATIONS EXERCISE - Chapter Test30videos
MISCELLANEOUS EQUATIONS AND INEQUATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - MEASURES OF CENTRAL TENDENCYEXERCISE - Chapter Test21videos
MEASURES OF CENTRAL TENDENCY
- BOOK - OBJECTIVE RD SHARMACHAPTER - PLANE AND STRAIGHT LINE IN SPACE EXERCISE - Chapter Test31videos
PLANE AND STRAIGHT LINE IN SPACE
Similar Questions
n-digit number
View SolutionLet an denote the number of all n-digit numbers formed by the digits 0,1 or both such that no consecutive digits in them are 0. Let bn be the number of such n-digit integers ending with digit 1 and let cn be the number of such n-digit integers ending with digit 0. Which of the following is correct ?
View SolutionLet an denote the number of all n-digit positive integers formed by the digits 0, 1, or both such that no consecutive digits in them are 0. Let bn=The number of such n-digit integers ending with digit 1 and cn= Then number of such n-digit integers with digit 0.
The value of b6 isView SolutionLet an denote the number of all n-digit positive integers formed by the digits 0, 1, or both such that no consecutive digits in them are 0. Let bn=The number of such n-digit integers ending with digit 1 and cn= Then number of such n-digit integers with digit 0.
The value of b6 isView SolutionLet an = number of n-digit positive integers formed by the digits 0, 1 or both such that no consecutive digits in them is 0.
Let bn = number of such n digit integers ending with digit 1, and cn = the numner of such n digit integers ending with digit 0, then for n≥3,View SolutionIf N is the number of three digit numbers of the form abc such that a<b<c then
View SolutionHow many numbers of n digits can be made with the non-zero digits in which no two consecutive digits are the same ?
View SolutionThe number of 'n' digit numbers such that no two consecutive digits are same is
View SolutionFind the total number of n -digit number (n>1) having property that no two consecutive digits are same.
View SolutionLet N be the number of 4 digit numbers formed with at most two distinct digits. Then the last digit of N is
View Solution