Question

Let ${\displaystyle A=\{x:-1\le x\le 1\}=B}$ be a function ${\displaystyle f:A\to B.}$ Then find the nature of each of the following functions.
(i) ${\displaystyle f\left(x\right)=\left|x\right|\text{(ii)}f\left(x\right)=x\left|x\right|}$
(iii) ${\displaystyle f\left(x\right)=x^3\text{(iv)}f\left(x\right)=\text{sin}\frac{\pi x}{2}}$

Explanation

(i) `f: [-1,1] to [-1,1], " where " f(x)=|x|`.
Graph of the function is as shown in the following figure.

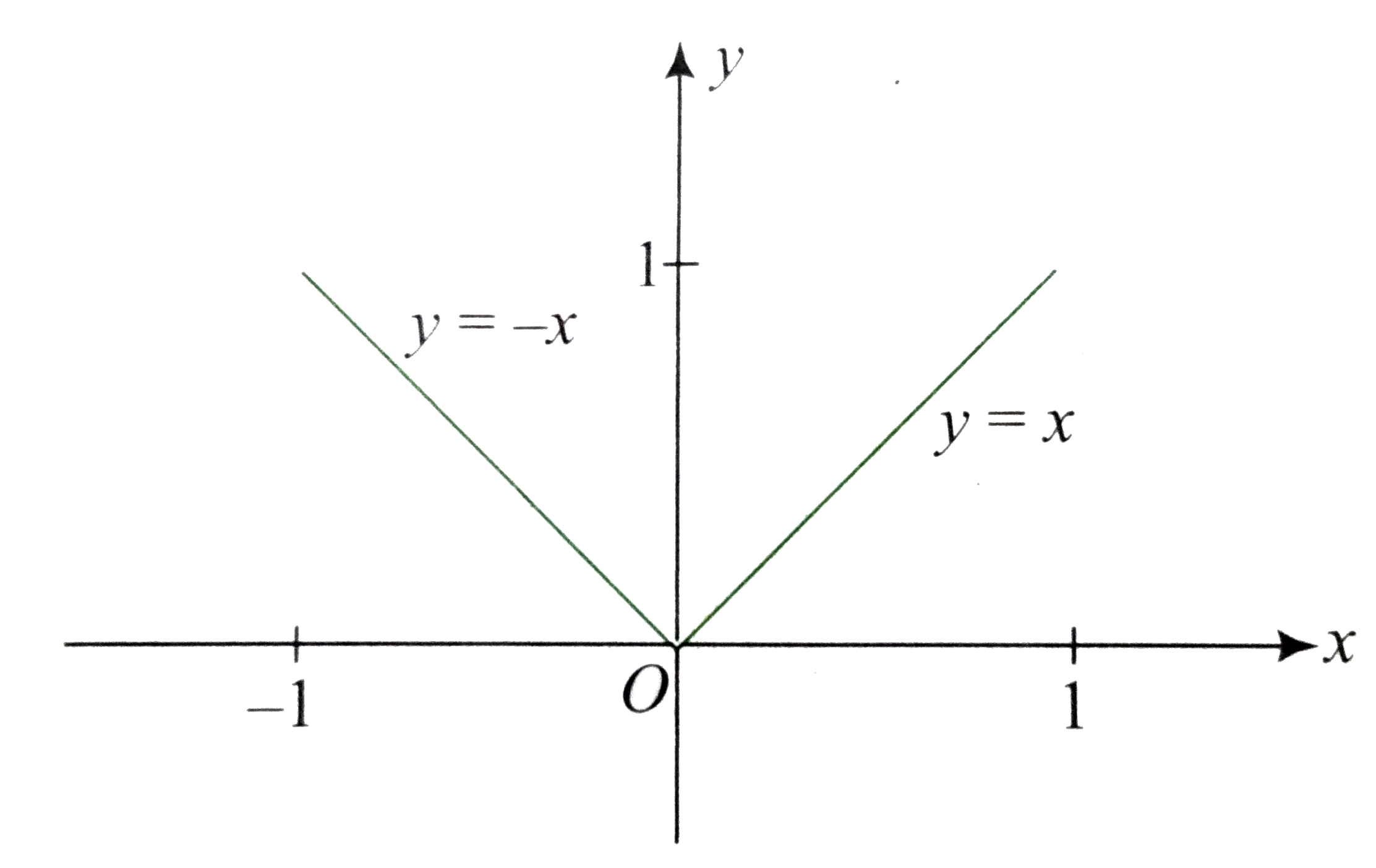
From the graph we observe that f(x) is many-one.
Also, we observe that the range is `[0,1]`. Hence f(x) is into.
(ii) `f:[-1,1] to [-1,1],` where `f(x)=x|x|`
Now `f(x)=x|x|={(x xx x", " x ge0),(x xx(-x)", " x lt 0):}={(x^(2)", " x ge0),(-x^(2)", " x lt 0):}`

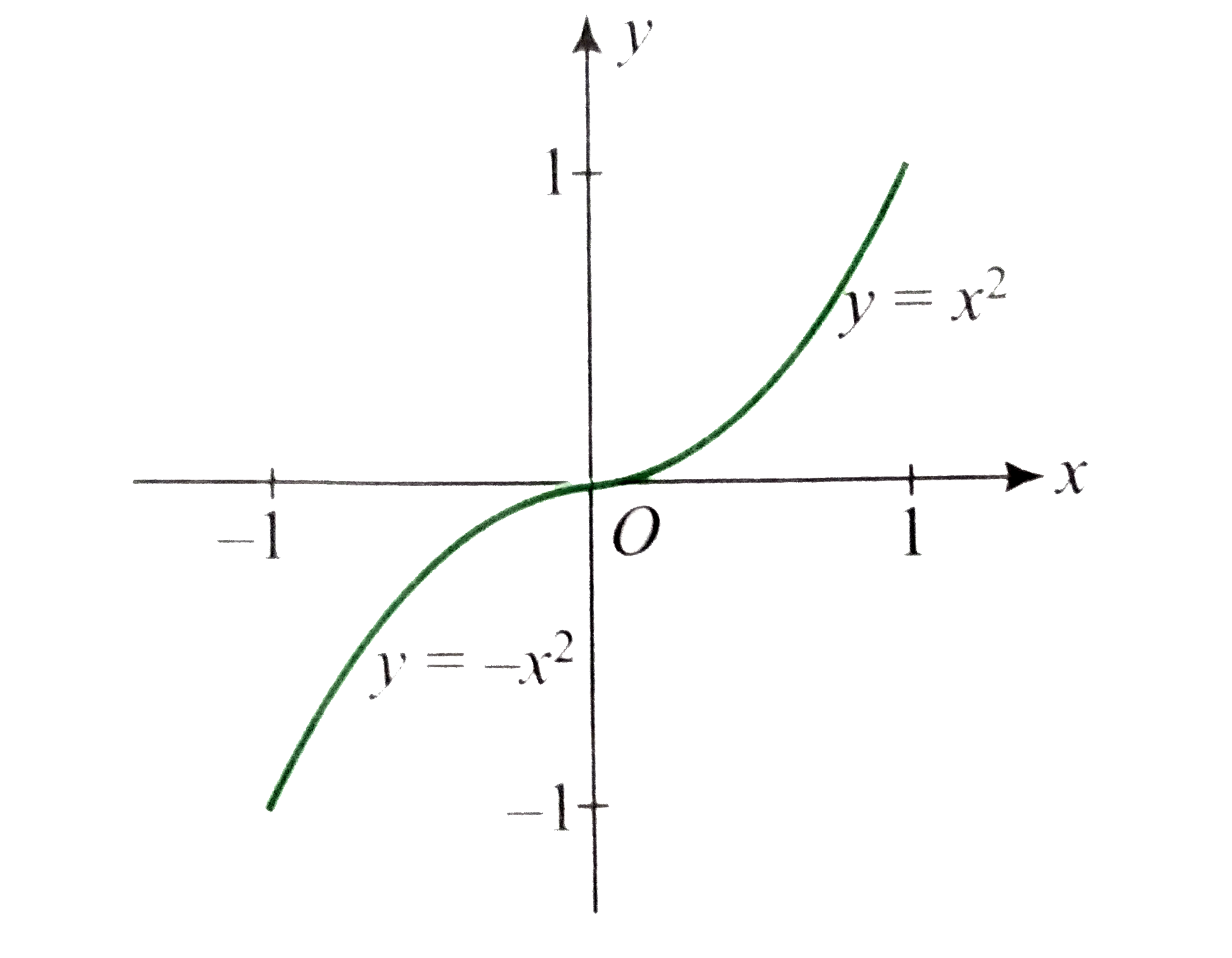
From the graph we observe that f(x) is one-one as there is no horizontal line which intersect the curve more than once.
Also, we observe that the range is `[-1,1]`. Hence f(x) is onto.
Thus f(x) is bijective.
(iii) `f: [-1,1] to [-1,1], " where " f(x) =x^(3)`

Clearly, f(x) is one-one.
Also, for `x in [-1,1], x^(3) in [-1,1].`
So, f(x) is onto.
Thus, f(x) is bijective.
(iv) `f:[-1,1] to [-1,1], " where "f(x) ="sin"(pi x)/(2)`
For ` x in [-1,1], (pi x)/(2) in [-(pi)/(2),(pi)/(2)]`
So, graph of f(x) is as shown in the following figure.

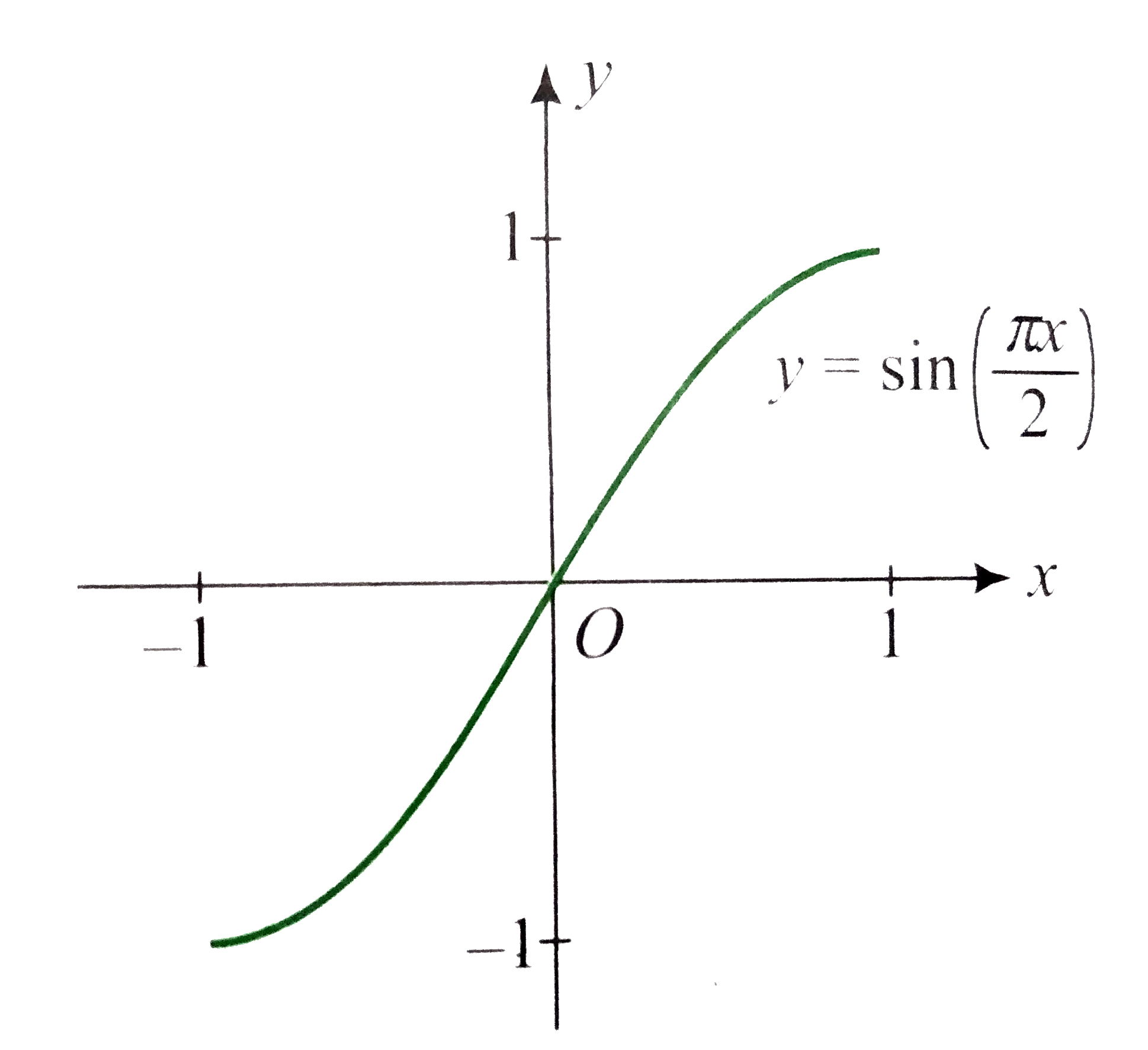
From the graph we observe that f(x) is one-one.
Also, range of the f(x) is `[-1,1].` Hence f(x) is onto.
Thus, f(x) is bijective.