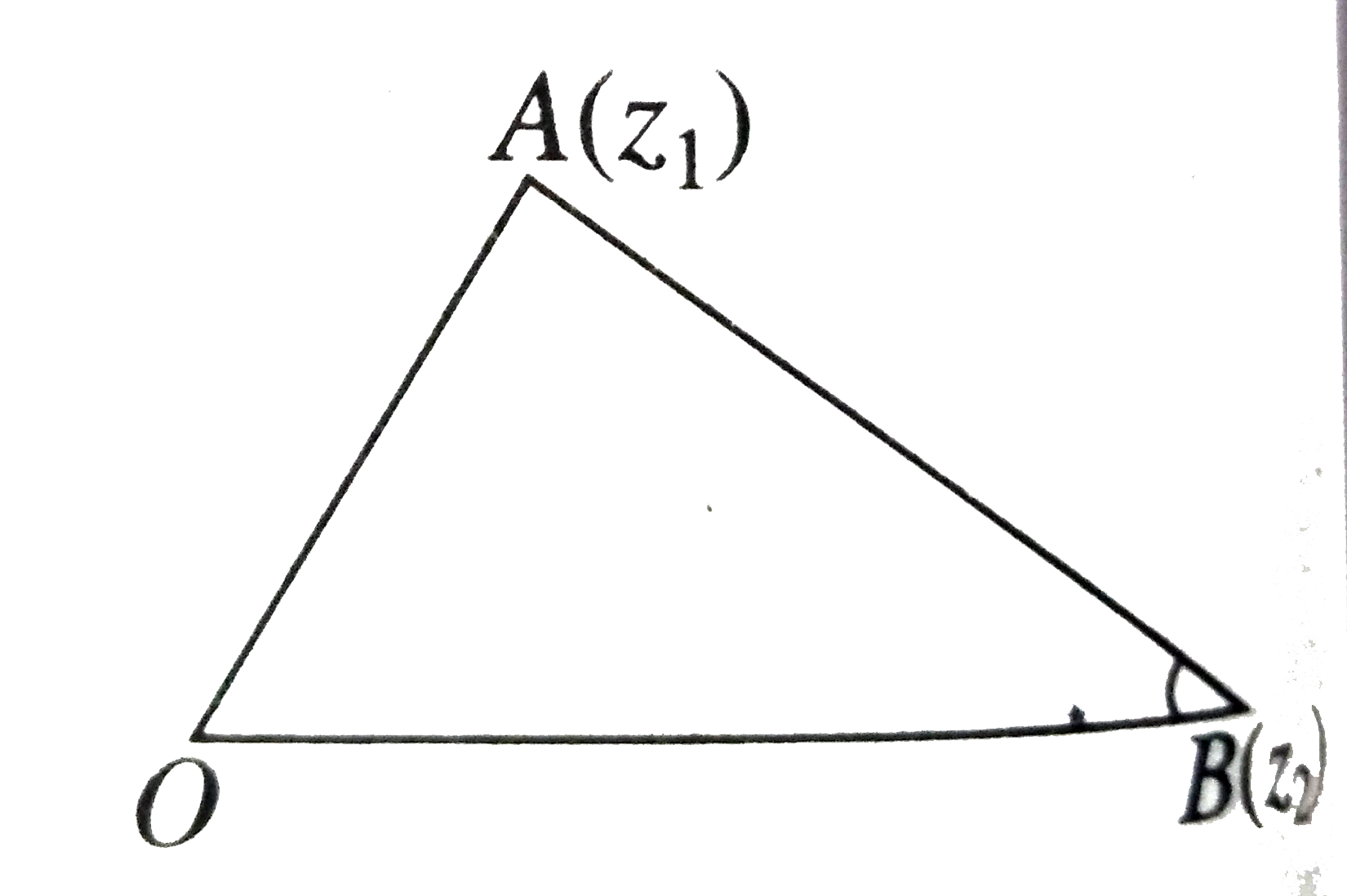
Let A(z1) and B(z2) are two distinct non-real complex numbers in the argand plane such that z1z2+¯z1z2=2. The value of |∠ABO| is
A
π6
B
π4
C
π2
D
None of these
Video Solution
Text Solution
The correct Answer is:C
(c) z1z2+¯z1¯z2=2
⇒Re(z1z2)=1
Let z1z2=x+iy⇒x=1
Now, arg(z1−z2−z2)=arg(1−z1z2)=arg(−iy)=±π2
∠ABO=π2
|
Topper's Solved these Questions
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Matching Column
1 Video
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Comprehension
11 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Question Bank
30 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
- CONIC SECTIONSBOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises
91 Videos
Similar Questions
Knowledge Check
For two complex numbersz1andz2 , we have ∣∣∣z1−z21−¯z1z2∣∣∣=1, then
Aboth z1andz2 lie on circle |z|=1Barg(z1z2)=π3CAt least one of z1andz2 lies on the circle |z|=1D|z1|=2|z2|Let z1andz2 be two non-zero complex number such that |z1|=|z2|=∣∣ ∣∣1z1+1z2∣∣ ∣∣=2
What is the value of |z1+z2| ?A8B4C2D1If z1andz2 are two distinct non-zero complex number such that |z1|=|z2|, then z1+z2z1−z2 is always
Apurely realBpurely imaginaryCequal to zeroDNone of these
If z1andz2, are two non-zero complex numbers such tha |z1+z2|=|z1|+|z2| then arg(z1)−arg(z2) is equal to
View SolutionIf z1andz2 are two complex numbers such that ∣∣∣z1−z2z1+z2∣∣∣=1, then
View SolutionIf z1 and z2 are two complex numbers such that ∣∣∣z1−z2z1+z2∣∣∣=1, then
View SolutionIf z1 and z2 are two complex numbers such that |z1|<1<|z2|, then prove that |(1−z1¯z2)/(z1−z2)|<1
View SolutionIf A(z1) and B(z2) are two fixed points in the Argand plane the locus of point P(z) satisfying |z−z1|+|z−z2|=|z1−z2|, is
View Solution