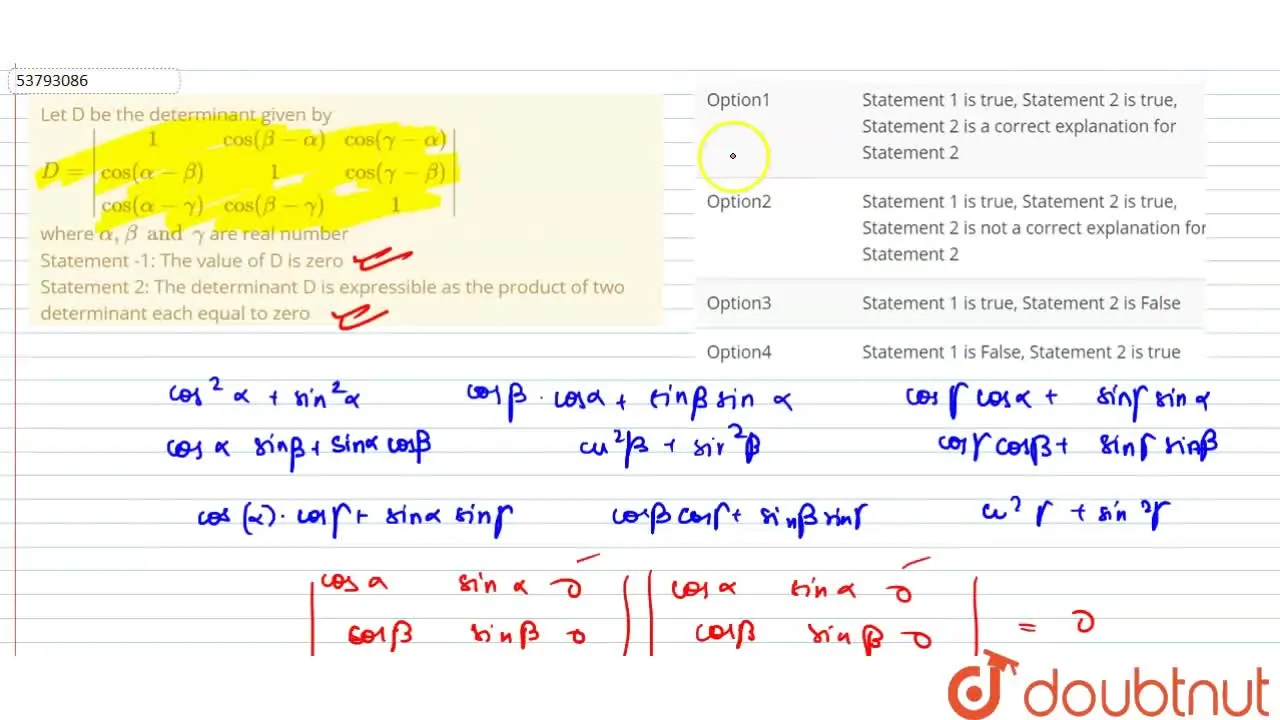
Let D be the determinant given by
D=∣∣
∣
∣∣1cos(β−α)cos(γ−α)cos(α−β)1cos(γ−β)cos(α−γ)cos(β−γ)1∣∣
∣
∣∣
where α,βandγ are real number
Statement -1: The value of D is zero
Statement 2: The determinant D is expressible as the product of two determinant each equal to zero
Statement 1 is true, Statement 2 is true, Statement 2 is a correct explanation for Statement 2
Statement 1 is true, Statement 2 is true, Statement 2 is not a correct explanation for Statement 2
Statement 1 is true, Statement 2 is False
Statement 1 is False, Statement 2 is true
The correct Answer is:A
We have,
D=∣∣
∣
∣∣1cos(β−α)cos(γ−α)cos(α−β)1cos(γ−β)cos(α−γ)cos(β−γ)1∣∣
∣
∣∣
=∣∣
∣
∣∣cos2α+sin2αcosβcosα+sinβsinαcosγcosα+sinγsinαcosαcosβ+sinαsinβcos2β+sin2βcosγcosβ+sinγsinβcosαcosγ+sinαsinγcosβcosγ+sinβsinγcos2γ+sin2γ∣∣
∣
∣∣
=∣∣
∣
∣∣cosαsinα0cosβsinβ0cosγsinγ0∣∣
∣
∣∣∣∣
∣
∣∣cosαsinα0cosβsinβ0cosγsinγ0∣∣
∣
∣∣=0
So, both the statement are true and statement 2 is a correct explanation for statement 1
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - DETERMINANTSEXERCISE - Exercise94videos
DETERMINANTS
- BOOK - OBJECTIVE RD SHARMACHAPTER - DETERMINANTSEXERCISE - Chapter Test30videos
DETERMINANTS
- BOOK - OBJECTIVE RD SHARMACHAPTER - DETERMINANTSEXERCISE - Section I - Solved Mcqs74videos
DETERMINANTS
- BOOK - OBJECTIVE RD SHARMACHAPTER - CONIC SECTIONSEXERCISE - Section I - Solved Mcqs1videos
CONIC SECTIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - DISCRETE PROBABILITY DISTRIBUTIONSEXERCISE - Exercise40videos
DISCRETE PROBABILITY DISTRIBUTIONS
Similar Questions
If α,βandγ are real number without expanding at any stage prove that
∣∣ ∣ ∣∣1cos(β−α)cos(γ−α)cos(α−β)1cos(γ−β)cos(α−γ)cos(β−γ)1∣∣ ∣ ∣∣=0.View Solution∣∣ ∣ ∣∣1cos(β−α)cos(γ−α)cos(α−β)1cos(γ−β)cos(β−α)cos(β−γ)1∣∣ ∣ ∣∣=
View SolutionIf α,β&γ real numbers, then value of ∣∣ ∣ ∣∣1cos(β−α)cos(γ−α)cos(α−β)1cos(γ−β)cos(α−γ)cos(β−γ)1∣∣ ∣ ∣∣ is equal to
View SolutionIf cos(β−γ)+cos(γ−α)+cos(α−β)=−32 then
View SolutionIf α,βandγ are real number without expanding at any stage prove that
∣∣ ∣ ∣∣1cos(β−α)cos(γ−α)cos(α−β)1cos(γ−β)cos(α−γ)cos(β−γ)1∣∣ ∣ ∣∣=0.View Solutioncos(α+β)cosγ−cos(β+γ)cosα=sinβsin(γ−α)
View SolutionProve that : cos2(β−γ)+cos2(γ−α)+cos2(α−β)=1+2cos(β−γ)cos(γ−α)cos(α−β).
View SolutionIf cos(α+γ)cos(α−γ)=cos2β then tanα,tanβandtanγ are
View SolutionIf cosα+cosβ+cosγ=0; then prove that cos3α+cos3β+cos3γ=12cosαcosβcosγ
View SolutionIf cosα+cosβ+cosγ=0 , then prove that cos3α+cos3β+cos3γ=12cosαcosβcosγ
View Solution