Let f:A→B, and let IA and IB be identity functions on A and B respectively. Prove that (foIA)=f and (IBof)=f
Let x∈A and let f(x) = y. Then
(foIA)(x)=f{IA(x)}=f(x)[∵IA(x)=x]
∴(foIA)=f.
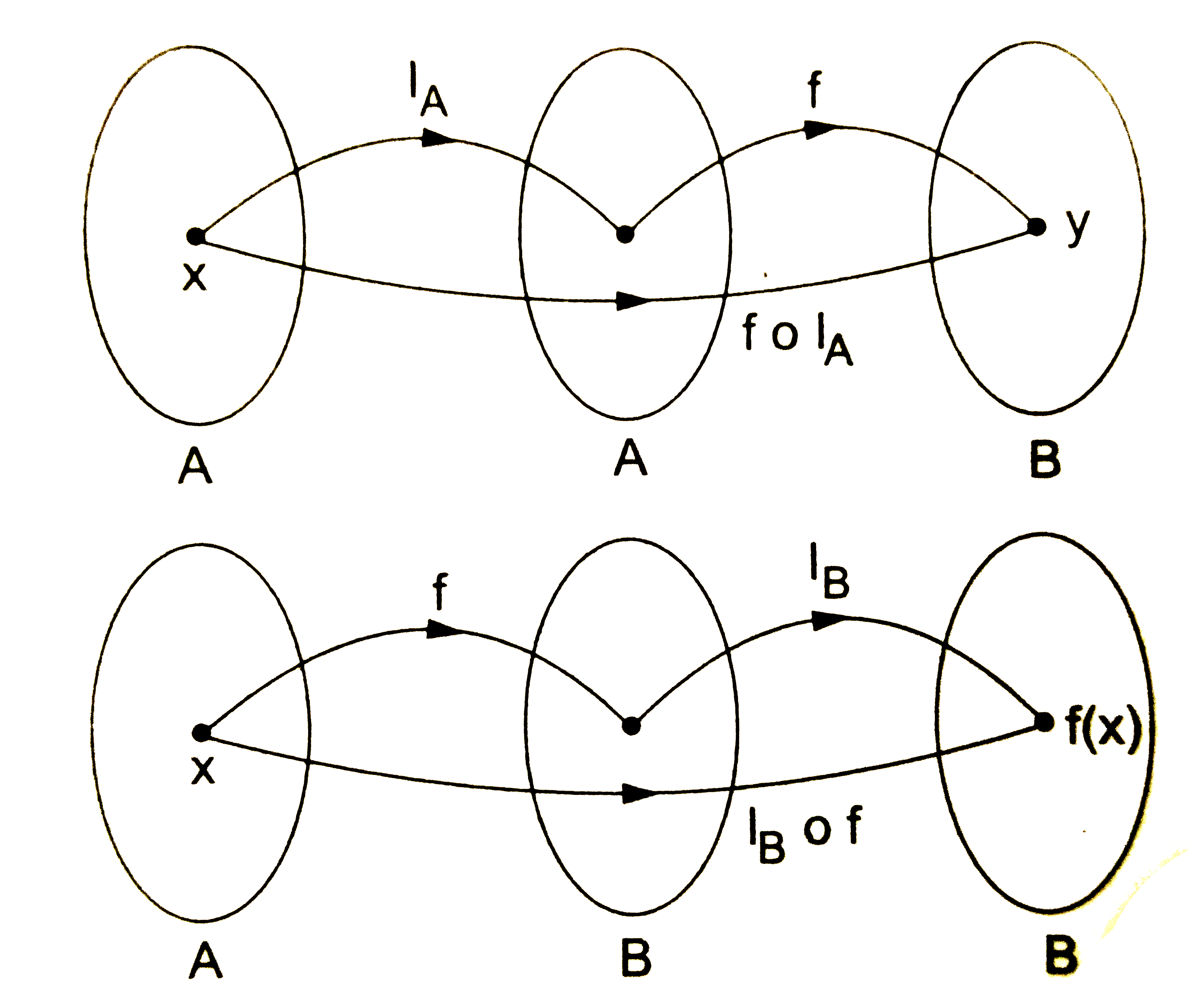
And (IBof)(x)=IBf(x)}
=IB(y)[∵f(x)=y]
=y[∵IB(y)=y]
=f(x)[∵y=f(x).]
∴(IBof)=f.
Hence (foIA)=f and (IBof)=f
Topper's Solved these Questions
- FUNCTIONSBOOK - RS AGGARWALCHAPTER - FUNCTIONSEXERCISE - Objective Questions
39 Videos
- FUNCTIONSBOOK - RS AGGARWALCHAPTER - FUNCTIONSEXERCISE - Exercise 2A
17 Videos
- DIFFERENTIATIONBOOK - RS AGGARWALCHAPTER - DIFFERENTIATIONEXERCISE - Exercise 10I
51 Videos
- FUNDAMENTAL CONCEPTS OF 3-DIMENSIONAL GEOMETRYBOOK - RS AGGARWALCHAPTER - FUNDAMENTAL CONCEPTS OF 3-DIMENSIONAL GEOMETRYEXERCISE - Exercise
18 Videos
Similar Questions
Let f:A→B, and let IA and IB be identity functions on A and B respectively. Prove that (foIA)=f and (IBof)=f
View SolutionLet A={a, b, c} , B={u v, w} and let f and g be two functions from A to B and from B to A respectively defined as: f={(a, v), (b, u), (c, w)} , g={(u, b), (v, a), (w, c)}. Show that f and g both are bijections and find fog and gof.
View Solution
Knowledge Check
Let f and g be differentiable functions on R such that fog is the identity function. If for some a,b∈R,g'(a)=5 and g(a)=b, then f'(b) is equal to :
A25B15C1D5Let f and g be differentiable function satisfying g'(a)=2,g(a)=bandg=f^(-1) then f' (b) is equal to
A1/2B2C2/3Dnone of these
Let A = {a, b, c, d}. The number of invertible functions f:A→A satisfying the following conditions:
f(d)=d,f(a)≠a,f(b)≠b is…………
View SolutionLet f be arry continuously differentiable function on [a,b] and twice differentiable on (a.b) such that f(a)=f(a)=0andf(b)=0. Then
View SolutionLet f and g be two functions such that gof=IA and fog=IB. Then; f and g are bijections and g=f−1
View Solution(Associativity ) Let f:A→B,g:B→C and h:C→. Then prove that ( h o g) o f = h o ( g o f )
View SolutionLet f:R→R:f(x)=|x| prove that f o f =f
View SolutionLet A=R−{3},B=R−{1}, and let f:A→B be defined by f(x)=x−2x−3 is f invertible? Explain.
View Solution
