Let 'f' be a non-zero real valued continuous function satisfying f(x + y) = f(x), f(y) . f(y) for all x,y∈R if f(2) = 9 , then f(6) = Solution in Telugu
32
36
34
33
The correct Answer is:B
Step by step video, text & image solution for Let 'f' be a non-zero real valued continuous function satisfying f(x + y) = f(x), f(y) . f(y) for all x, y in R if f(2) = 9 , then f(6) = by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LIMITS AND CONTINUITYBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - LIMITS AND CONTINUITYEXERCISE - Exercise 2(Special Type Questions)
10 Videos
- LIMITS AND CONTINUITYBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - LIMITS AND CONTINUITYEXERCISE - SET-3Match The Following
2 Videos
- LIMITS AND CONTINUITYBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - LIMITS AND CONTINUITYEXERCISE - Exercise 1B( One Sided Limits)
71 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) (SET - 4)
5 Videos
- LINEAR PROGRAMMING [APPENDIX-2]BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - LINEAR PROGRAMMING [APPENDIX-2]EXERCISE - Exercise -1
33 Videos
Similar Questions
I. Ltx→0(1+x)2−(1−x)2−2(1+x)3−(1−x)3−3
II. If f(x)=4−7x3x+4andLtx→2f(x)=l,Ltx→0f(x)=m then the equation whose roots are 1/l, 1/m is x2−1=0
View SolutionMatch the following
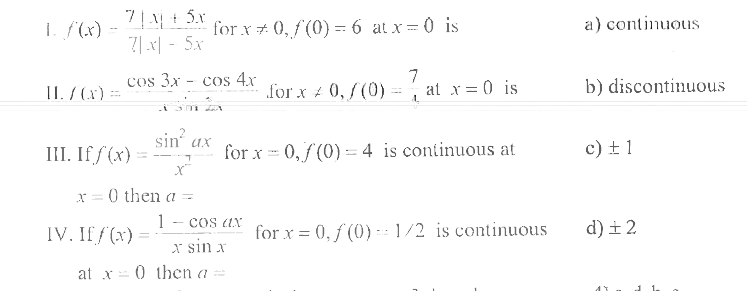
View SolutionLtx→0√x=
View SolutionA : The maximum value of f(x)=Sin−1x+Cos−1x−Tan−1x is 3π/4
R : Sin−1x+Cos−1x=π/2∀x∈R
View SolutionIf 2x+y≥10,x+2y≥10, then the lesat value of F=x+y is
View SolutionIf f is a real valued function not identically zero,satisfying f(x+y)+f(x-y)=2f(x)*f(y) then f(x)
View SolutionIf a real valued function f(x) satisfies the equation f(x+y)=f(x)+f(y) for all x,y in R then f(x) is
View SolutionLet a real valued function f satisfy f(x+y)=f(x)f(y)∀x,y∈Randf(0)≠0 Then g(x)=f(x)1+[f(x)]2 is
View SolutionLet f be a real valued function satisfying f(x+y)=f(x)+f(y) for all x,y∈Randf(1)=2. Then n∑k=1f(k)=
View SolutionLet f be a real valued function satisfying
f(x+y)=f(x)f(y) for all x,y∈R such that f(1)=2.
Then , n∑k=1f(k)=
View SolutionLet f(x) be a real valued function such that f(0)=12 and f(x+y)=f(x)f(a-y)+f(y)f(a-x),∀x,y∈R, then for some real a,
View SolutionLet f be a real valued function, satisfying f(x+y)=f(x)f(y) for all a,y ∈R Such that,f(1=a.Then,f(x)=
View SolutionLet f be a non zero continuous function satisfying f(x+y)=f(x) f(y) for all x,y∈R. If f(2)=9 then f(3) is
View SolutionLet f be a non - zero real valued continuous function satisfying f(x+y)=f(x)f(y) for x,y∈R If f(2)=9 the f(6)=
View SolutionLet f be function satisfying f(x+y)=f(x)+f(y) and f(x)=x2g(x), for all x and y, where g(x) is a continuous function. Then f'(x) is :
View Solution
