Question

Let $f:R\to R$
be a continuous onto function satisfying $f\left(x\right)+f(-x)=0\forall x\in R$.

If $f(-3)=2andf\left(5\right)=4in[-5,5],$
then the minimum number of roots of the equation $f\left(x\right)=0$
is

Answer

3

Explanation

`f(x)+f(-x)=0`
Therefore,`f(x)` is an odd function.
Since points (-3, 2) and (5, 4) lie on the curve,
` :. ` (3, -2) and (-5, -4) will also lie on the curve.
For minimum number of roots, graph of continuous function `f(x)` is as follows:

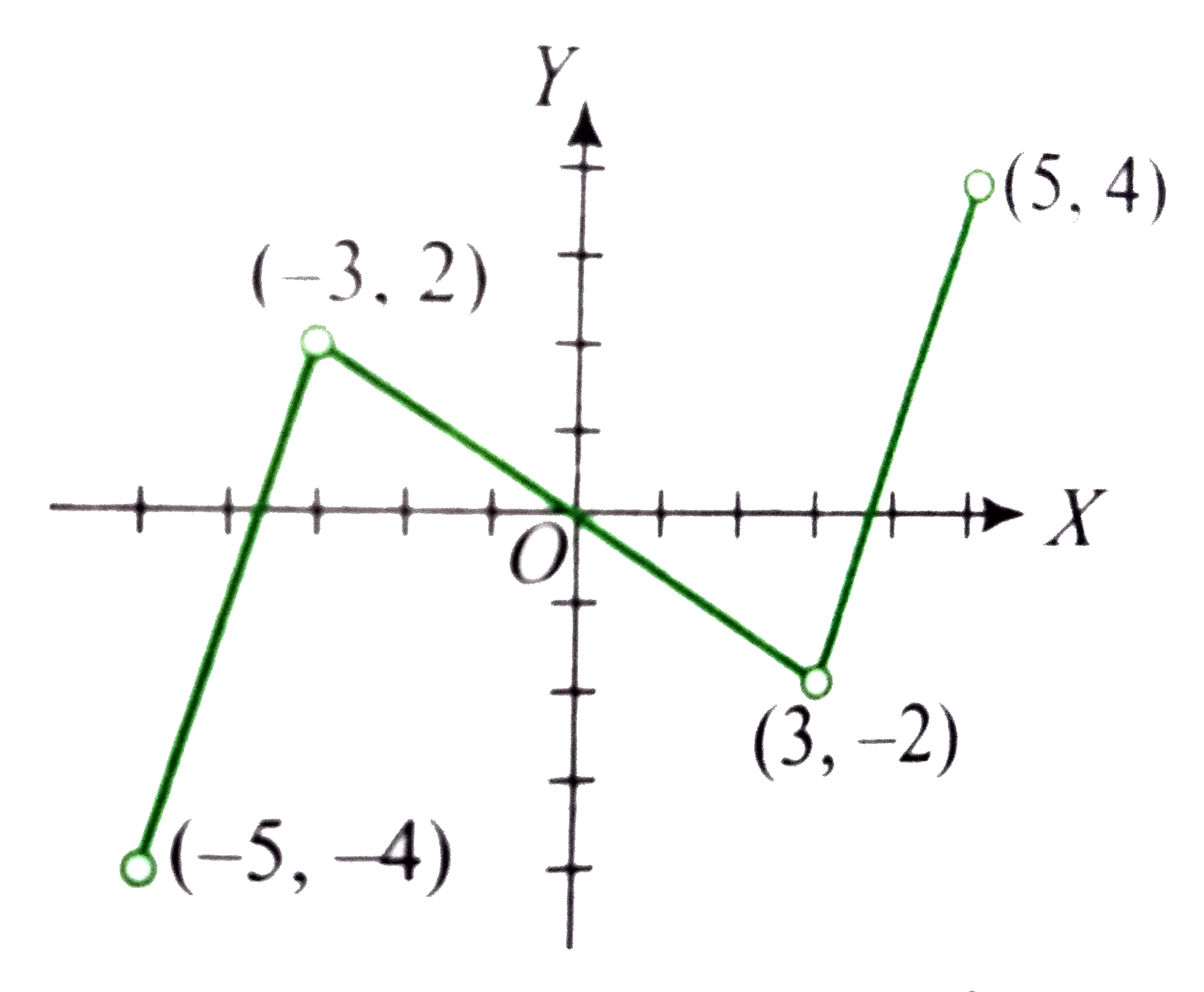
From the above graph of `f(x)`, it is clear that equation `f(x)=0` has at least three real roots.