Let f:R→R be a differentiable function such that f (a) = 0 = f (b) and f'(a)f'(b)>0 for some a<b. Then the minimum number of roots of f'(x) 0 in the interval (a, b) is
3
2
1
0
The correct Answer is:B
f'(a).f'(b)>0
so either both are positive or both negative
f(a)=f(b)=0
f'(x)=0
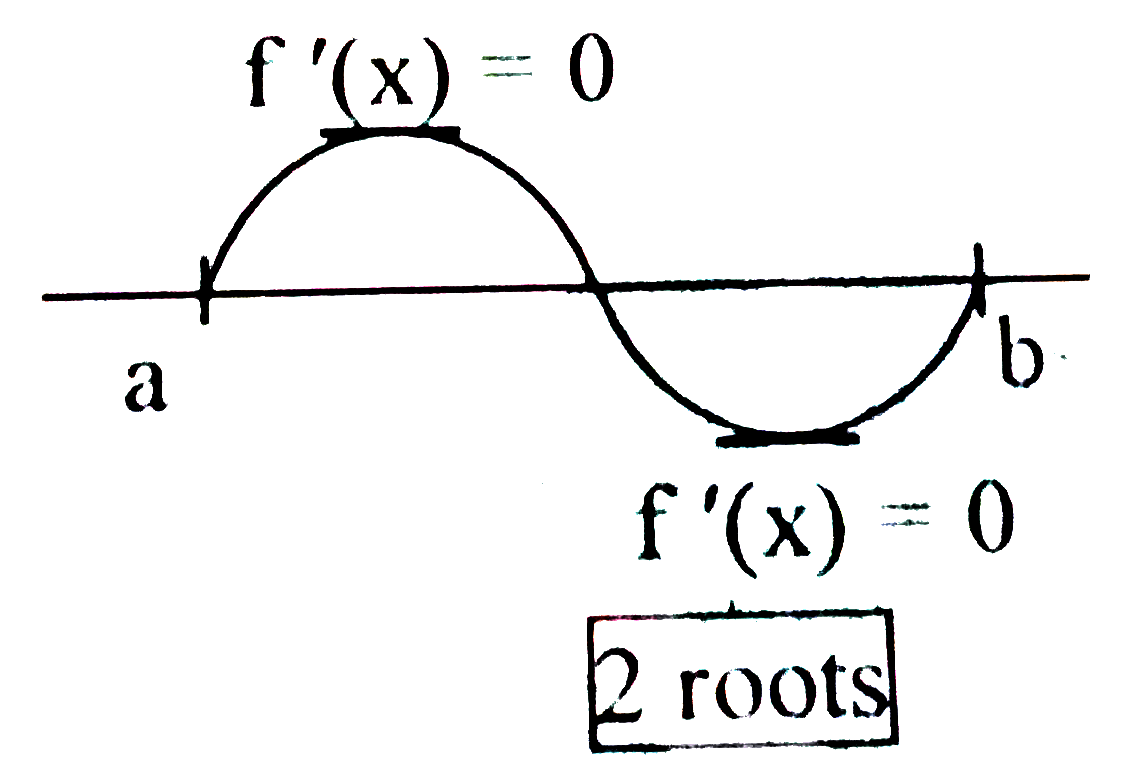
2 roots
Topper's Solved these Questions
Similar Questions
Let f:R→R be a differentiable function such that f (a) = 0 = f (b) and f'(a)f'(b)>0 for some a<b. Then the minimum number of roots of f'(x) 0 in the interval (a, b) is
View SolutionIf f(x) is a twice differentiable function such that f(a)=0, f(b)=2, f(c)=-1,f(d)=2, f(e)=0 where a < b < c < d e, then the minimum number of zeroes of g(x)=f'(x)2+f''(x)f(x) in the interval [a, e] is
View Solution
Knowledge Check
Let f be a differentiable function defined on R such that f(0) =−3. If f'(x) ≤5 for all x then
Af(2)>7Bf(2)≤7Cf(2)>8Df(2)=8f and g differentiable functions of x such that f(g(x))=x, If g'(a)≠0 and g(a)=b, then f'(b)=
Ag(a)B1g(a)C−g'(a)D1g'(a)If f(x)>0 and differentiable in R, then :f'(x)=
Af(x)⋅ddx[ef(x)]Bf(x)⋅ddx[elogf(x)]Cf(x)⋅ddx[logf(x)]Def(x)
Let f(x) is a continuous function such that f(−1)=−2,f(0)=−1,f(1)=0,f(2)=1,f(3)=0,f(4)=−1andf(5)=1 then minimum number of roots of f'(x)+xf(x)=0 in the interval (−1,5) are
View SolutionLet f:R→R be a twice differentiable function such that f(x+π)=f(x) and fx+f(x)≥0 for all x∈R. Show that f(x)≥0 for all x∈R.
View SolutionFor all twice differentiable functions f:R→R , with f(0)=f(1)=f'(0)=0
View SolutionLet f:R→R be a differential function satisfy f(x)=f(x−y)f(y)∀x,y∈R and f'(0)=a,f'(2)=b then f'(−2)=
View SolutionLet f:[a,b]→Rbe differentiable on [a,b]&k∈R. Let f(a)=0=f(b). Also let J(x)=f'(x)+kf(x). Then
View Solution
