Let such that Where are polynomials of least possible degree and has leading coefficient unity. Then match the following Column-I with Column-II.
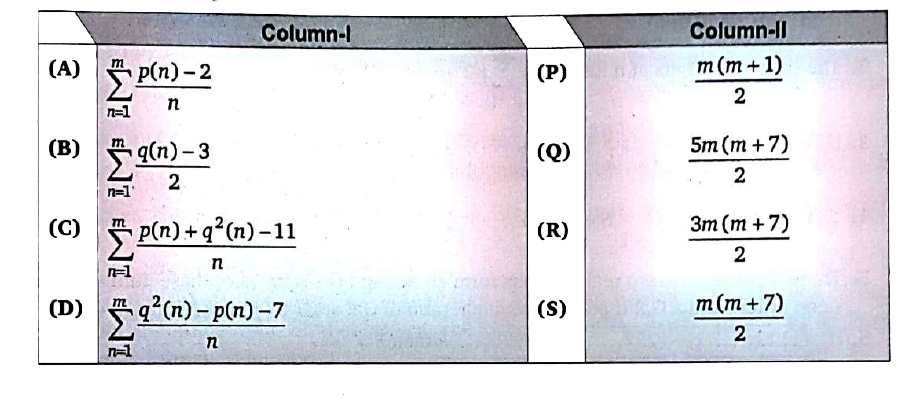
Text Solution
The correct Answer is:
|
Topper's Solved these Questions
- SEQUENCE AND SERIES BOOK - VK JAISWALCHAPTER - SEQUENCE AND SERIES EXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)
21 Videos
- SEQUENCE AND SERIES BOOK - VK JAISWALCHAPTER - SEQUENCE AND SERIES EXERCISE - EXERCISE (COMPREHENSION TYPE PROBLEMS)
17 Videos
- QUADRATIC EQUATIONS BOOK - VK JAISWALCHAPTER - QUADRATIC EQUATIONS EXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)
45 Videos
- SOLUTION OF TRIANGLESBOOK - VK JAISWALCHAPTER - SOLUTION OF TRIANGLESEXERCISE - Exercise-5 : Subjective Type Problems
13 Videos
Similar Questions
Knowledge Check
Let P(x)=a0xn+a1xn−1+...+an(n∈N). Then degree of polynomial is (an≠0)
AnB1Cnot definedDeither n or less than nIf 2n+1Pn−1:2n−1Pn=3:5the possible value of n will be :
A3B5C4D2
If f(x)=(p−xn)1n ,p>0 andn is a positive integer then f[f(x)] is equal to
View SolutionFind n if :
2n+1Pn−1:2n−1Pn=3:5
View SolutionIf P(n):1+4+7…….+(3n−2)=12n(3n−1).Verify P(n) for n =1,2.
View SolutionIf f(x)=(p−xn)1n ,p>0 andn is a positive integer then f[f(x)] is equal to
View SolutionIf n is a natural number and we define a polynomial pa(x) of degree n such that cosnθ=pn(cosθ), then The value of pn+1(x)+pn−1(x)=
View SolutionLet f(n)=1+12+13++1n. Then f(1)+f(2)+f(3)++f(n) is equal to
(a)nf(n)−1
(b) (n+1)f(n)−n
(c)(n+1)f(n)+n
(d) nf(n)+n
View Solution
