Let f (x) be a function defined by f(x)=∫x0t(t2−3t+2)dt,1≤,x≤3.
Then, the range of f(x) is

A

[0,2]

B

[-1/4,4]

C

[-1/4,2]

D

none of these

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C

We have ,
f(x)=x∫1(t3−3t2+2t)dt
⇒f'(x)=x3−3x2+2x=x(x−2)(x−1)
The changes in sings of f'(x) for different values of x are given in Fig. 11
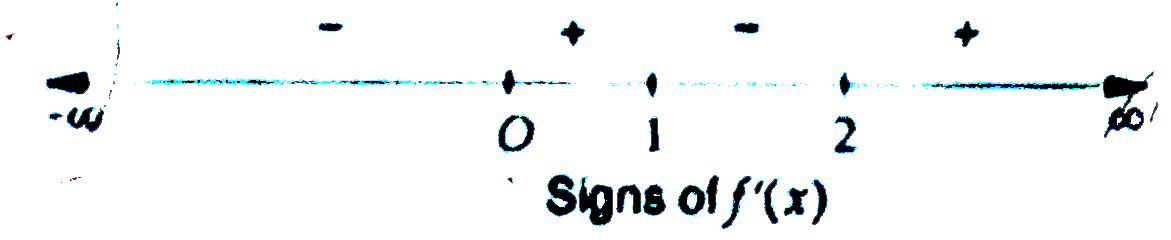
ocr_image
Clearly, f(x) is decreasing in [1,2] and increasing in [2,3]
∴Minf(x)=f(2)=2∫1t(t2−3t+2)dt=[t44=t3+t2]21=−14 and
∴Maxf(x)=f(3)=2∫1t(t2−3t+2)dt=[t44=t3+t2]31=2
Since f(x) is continuous on [1,3]. Therefore, range of f(x)=[f(2),f(3)]=[−1/4,2]

Updated on:21/07/2023
|
Class 12MATHSDEFINITE INTEGRAL

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Let f(x) be a function defined by
    f(x)=∫x1t(t2−3t+2)dt,x∈[1,3]
    Then the range of f(x), is

    A[0,2]
    B[−14,4]
    C[−14,2]
    Dnone of these

  • Let f(x)=∫x2f(t2−3t+4)dt. Then

    Af(2) = 0
    Bf(−2)=0
    Cf'(2)=0
    Df'(2)=2

  • If f(x) =∫x2x(t−1)dt,1≤x≤2 then the greatest value of ϕ (x) , is

    A2
    B4
    C8
    Dnone of these