Let f (x) be a polynomial function of degree 3 where a<b<candf(a)=f(b)=f(c). If the graph of f (x) is as shown, which of the following statements are INCORRECT ? (Where c>|a|)
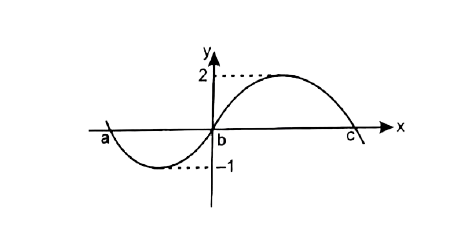
(a) ∫caf(x)dx=∫cbf(x)dx+∫bcf(x)dx
(b) ∫caf(x)dx<a
(c) ∫baf(x)dx<∫bcf(x)dx
(d) 1b−a∫baf(x)dx>1c−b∫cbf(x)dx
The correct Answer is:B, C, D
Step by step video & image solution for Let f (x) be a polynomial function of degree 3 where a lt b lt c and f (a) =f (b) = f(c ). If the graph of f (x) is as shown, which of the following statements are INCORRECT ? (Where c gt|a|) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREA UNDER CURVESBOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - AREA UNDER CURVESEXERCISE - AXERCISE (COMPREHENSION TYPE PROBLEMS)
6 Videos
- AREA UNDER CURVESBOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - AREA UNDER CURVESEXERCISE - AXERCISE (MATCHING TYPE PROBLEMS)
1 Videos
- AREA UNDER CURVESBOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - AREA UNDER CURVESEXERCISE - AXERCISE (SUBJECTIVE TYPE PROBLEMS)
8 Videos
- APPLICATION OF DERIVATIVES BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)
22 Videos
- BIONMIAL THEOREMBOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - BIONMIAL THEOREMEXERCISE - Exercise-4 : Subjective Type Problems
15 Videos
Similar Questions
Let f(x)=(x−a)(x−b)(x−c) be a ral vlued function where a<bc(a,b,c∈R) such that f''(α)=0. Then if α∈(c1,c2), which one of the following is correct ?
View SolutionIf f(x) is a polynomial function of the second degree such that, f(−3)=6,f(0)=6 and f(2)=11, then the graph of the function, f(x) cuts the ordinate x = 1 at the point
View Solution
Knowledge Check

The graphs shown above represent f(x) and f(x+a) + b, where a and b are constants. Which of the following is the ordered pair (a,b) ?A(1,2)B(2,1)C(-1,2)D(2,-1)
If f(x) is a polynomial of degree <3, then, f(x)(x−a)(x−b)(x−c)is equals to
View SolutionIf f(x) is a polynomial of degree n(>2) and f(x)=f(α−x),
(where α is a fixed real number ), then the degree of f'(x) is
View SolutionLet f be a real-valued function defined on interval (0,∞),by f(x)=lnx+∫x0√1+sint.dt. Then which of the following statement(s) is (are) true? (A). f"(x) exists for all ∈ (0,∞). (B). f'(x) exists for all x ∈ (0,∞) and f' is continuous on (0,∞), but not differentiable on (0,∞). (C). there exists α>1 such that |f'(x)|<|f(x)| for all x ∈ (α,∞). (D). there exists β>1 such that |f(x)|+|f'(x)|≤β for all x ∈ (0,∞).
View SolutionLet f(x)=g(x)h(x), where g and h are continuous functions on the open interval (a, b). Which of the following statements is true for a<x<b ?
View SolutionIf a<b<c∈R and f(a+b+c−x)=f(x) for all, x then ∫bax(f(x)+f(x+c))dxa+b is:
View SolutionIf a<b<c, then find the range of f(x)=|x−a|+|x−b|+|x−c|
View SolutionLet f(x) be a non - constant polynomial such that f(a)=f(b)=f(c)=2. Then the minimum number of roots of the equation f''(x)=0 in x∈(a,c) is/are
View Solution
