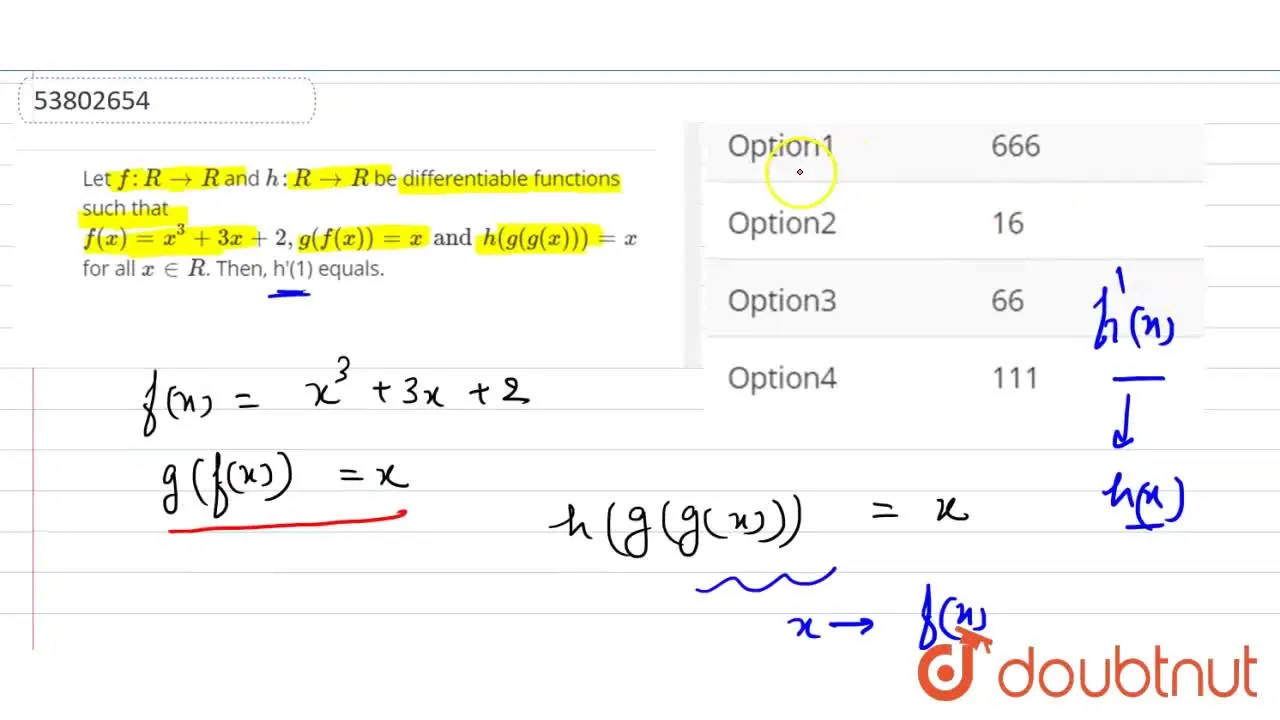
Let f:R→R and h:R→R be differentiable functions such that f(x)=x3+3x+2,g(f(x))=xandh(g(g(x)))=x for all x∈R. Then, h'(1) equals.
666
16
66
111
The correct Answer is:A
We have
g(f(x))=xandh(g(g(x))=xfor all x∈R
⇒h(g(g(f(x)))=f(x)for all x∈R [Replacing x by f(x)]
⇒h(g(x))=f(x)for all x∈R [∴g(f(x))=x]
⇒h(g(f(x)))=f(f(x))for all x∈R [Replacing x by f(x))]
⇒h(x)=f(f(x))for all x∈R [∴g(f(x))=x]
⇒h'(x)=f'(f(x))f'(x)for all x∈R
⇒h'(1)=f'(f(1))f'(1)=f'(6)f'(1) [∴f'(x)=3x2+3]
h'(1)=(3×26+3)(3+3)=666
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Section II - Assertion Reason Type13videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise86videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise86videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test59videos
COMPLEX NUMBERS
- BOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Chapter Test 260videos
DEFINITE INTEGRALS
Similar Questions
Let f:R→Randg:R→R be differentiable functions such that f(x)=x3+3x+2,g(f(x))=xfor all x∈R, Then, g'(2)=
View SolutionLet f:R→R,g:R→Randh:R→R be the differential functions such that f(x)=x3+3x+2,g(f(x))=xandh(g(g(x)))=x,forallx∈R.Then (a)g'(2)=115 (b)h'(1)=666 (c)h(0)=16 (d)h(g(3))=36
View SolutionLet f be a differentiable function such that f(0)=e2 and f'(x)=2f(x) for all x∈RIf h(x)=f(f(x)) ,then h'(0) is equal to
View SolutionLet f be a differentiable function such that f(1) = 2 and f'(x) = f (x) for all x∈R. If h(x)=f(f(x)), then h'(1) is equal to
View SolutionLet f be a differentiable function such that f(1)=2 and f'(x)=f(x) for all x∈R. If h(x)=f(f(x)) then h'(1) is equal to
View SolutionLet f:R→R and g:R→R be two functions such that fog(x)=sinx2andgof(x)=sin2x Then, find f(x)andg(x).
View SolutionLet f:R→Randg:R→R be two functions such that (gof)(x)=sin2xand(fog)(x)=sin(x2). Find f(x)andg(x).
View SolutionIf : R→R+ be a differentiable function and g(x)=e2x(2f(x)−3(f(x))2+2(f(x))3)forx∈R, then
View SolutionLet f and g be differentiable functions on R such that g(1)=3=g'(1) and f'(4)=118−π .If h(x)=f(3xg(x)+sin(πx)−5) then h'(1) is equal to
View SolutionLet f:R→R,g:R→R be two functions such that
f(x)=2x−3,g(x)=x3+5 The function (fog)−1(x) is equal toView Solution