Let f(x) be a function defined on (−a,a) with a gt 0. Assume that f(x) is continuous at x = 0 and limx→0f(x)−f(kx)x=α, where k∈(0,1) then
A
f'(0+)=0
B
f'(0−)=α1−k
C
f(x) is defferentiable at x = 0
D
f(x) is non-differentiable at x = 0
Video Solution
Text Solution
The correct Answer is:B, C, D
∵ limx→0f(x)−f(lα)x=α
⇒ limx→0f(x)−f(0)+f(0)−(kx)x=α
⇒ limx→0(f(x)−f(0)x−f(lx)−f(0)x)=α
⇒ (limx→0f(x)−f(0)x)−(limx→0f(kx)−f(0)kx)k=α
⇒ ⎧⎪
⎪
⎪⎨⎪
⎪
⎪⎩limx→0−f(x)−f(0)x−limx→0−f(kx)−f(0)kxk=αlimx→0+f(kx)−f(0)kx−limx→0+f(kx)−f(0)kx.k=α
={f'(0−)−kf'(0−)=αf'(0+)−kf'(0+)=α
={(1−k)f'(0−)=α(1−k)f'(0+)=α
={f'(0−)=α−kf'(0+)=α1−k
∴ f'(0)=f'(0−)=f'(0+)=α1−k
|
Topper's Solved these Questions
- CONTINUITY AND DIFFERENTIABILITYBOOK - CENGAGECHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Comprehension Type
2 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - CENGAGECHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Solved Examples And Exercises
108 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - CENGAGECHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Question Bank
22 Videos
- CONIC SECTIONSBOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises
91 Videos
- COORDINATE SYSTEMBOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
Similar Questions
Let f(x) be a function defined on (−a,a) with a>0. Assume that f(x) is continuous at x=0and(lim)x→0f(x)−f(kx)x=α,wherek∈(0,1) then f′(0+)=0 b. f′(0−)=α1−k c. f(x) is differentiable at x=0 d. f(x) is non-differentiable at x=0
View SolutionLet f''(x) be continuous at x = 0 and f"(0) = 4 then value of limx→02f(x)−3f(2x)+f(4x)x2
View Solution
Knowledge Check
Let f (x) be a conitnuous function defined on [0,a] such that f(a−x)=f(x)for allx∈[0,a]. If ∫a/20f(x)dx=α, then ∫a0f(x)dx is equal to
AαB2αC0Dnone of theseLet f be a function defined for every x, such that f''=−f,f(0)=0,f'(0)=1 then f(x) is equal to
Atan xBex−1Csin xD2 sin xIF the function f(x) defined by
f(x)=xsin1x for x≠0
=K for x=0
is continuous at x=0 , then k=A0B1C−1D12
If f(x) is continuous at x=0, then f(0) is defined as where
View SolutionIf f'(x)=f(x) and f(0)=1 then limx→0f(x)−1x=
View SolutionEvaluate limx→0f(x), where
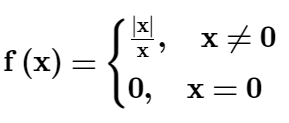
View SolutionLet f(x)be a derivable function, f'(x)>f(x) and f(0)=0. Then
View SolutionIf f(x) is continuous at x=0, where f(x)={1−cosxx, for x≠0k, forx=0, then k=
View Solution
