Let f(x)
be continuous function given by
f(x)={2x,|x|≤1and x2+ax+b,|x|>1}.
Find the area of the region in the third quadrant bounded by the curves
x=−2y2andy=f(x)
lying on the left of the line 8x+1=0.Solution in Bengali
sq. units
257192 sq. units
25796 sq. units
289192 sq. units
The correct Answer is:B
f(x)=⎧⎪⎨⎪⎩x2+ax+bx<−12x−1≤x≤1x2+ax+bx>1
∵ f(x)iscont∈uousatx=−1andx=1
∴ (−1)2+a(−1)+b=−2⇒b−a=−3 ...(1)
and 2=(1)2+a.1+b⇒a+b=1 ...(2)
Solving (1) and (2), we get a=2,b=−1
∴ f(x)=⎧⎪⎨⎪⎩x2+2x−1x<−12x−1≤x≤1x2+2x−1x>1
Given curves are y=f(x),x=−2y2and8x+1=0
Solving x=−2y2,y=x2+2x−1(x<−1) we get x=-2
Also, y=2x,x=−2y2 meet at (0,0)
y=2xandx=−1/8 meet at (−18,−14)
The required area is the shaded region in the figure
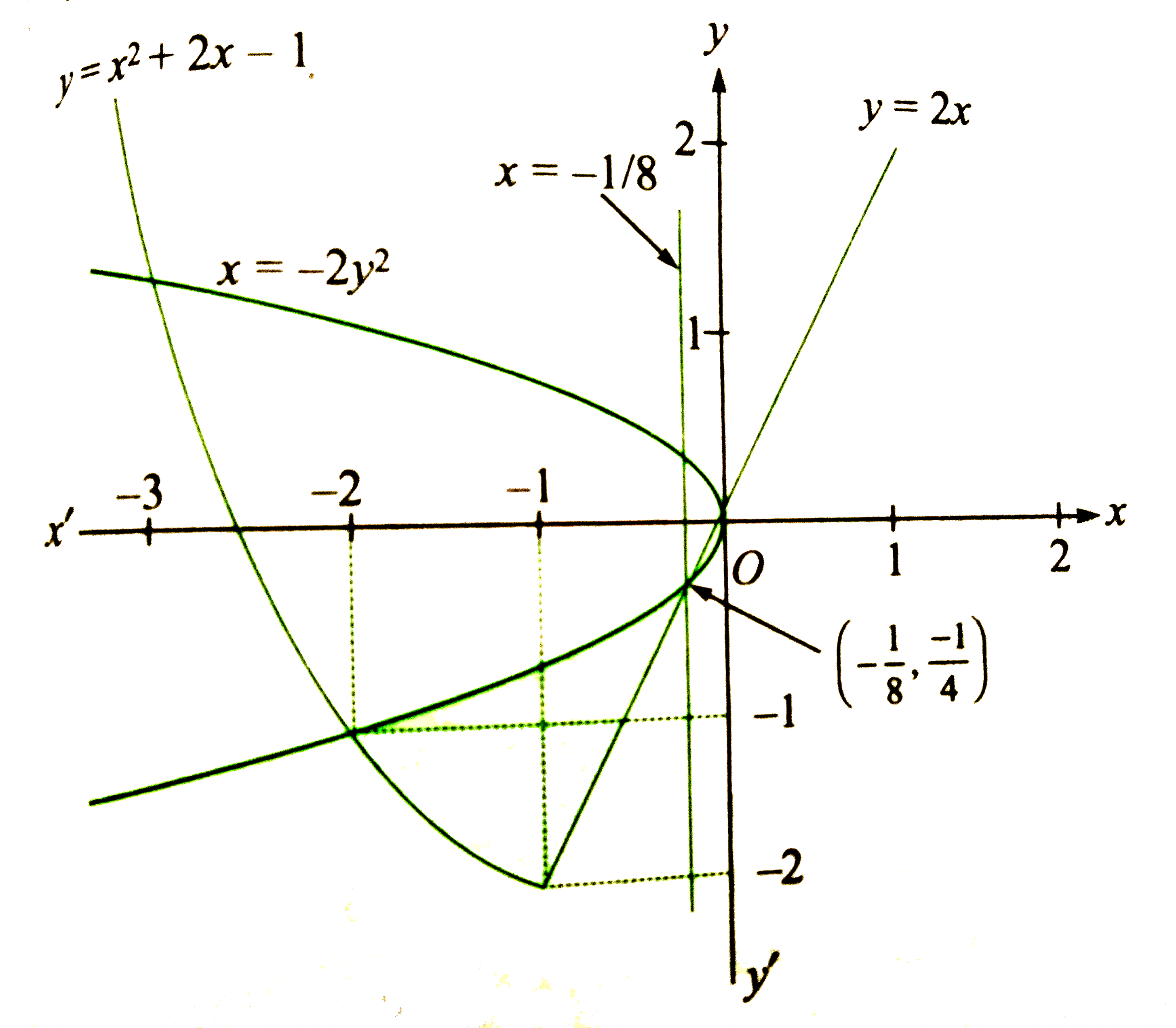
∴ Required area
=∫−1−2[−√−x2−(x2+2x−1)dx]+∫−1/8−1[−√−x2−2x]dx
=[1√22(−x)3/23−x33−x2+x]−1−2+[1√22(−x)3/23−x2]−1/8−1
=(√23+13−1−1)−(43+83−4−2)+(√23.116√2−164)−(√23−1)
=(√2−53)−(4+8−183)+(4−3192)−(√2−33)
=257192 sq. units
Topper's Solved these Questions
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Matrix Match Type
5 Videos
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Numerical Value Type
18 Videos
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Multiple Correct Answers Type
13 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
Similar Questions
Match the following lists :

View SolutionThe area enclosed by the curve c:y=x√9−x2(x≥0) and the x-axis is________
View SolutionLet A(k) be the area bounded by the curves y=x2−3 and y=kx+2 The range of A(k) is (10√53,∞) The range of A(k) is (20√53,∞) If function k→A(k) is defined for k∈[−2,∞ ), then A(k) is many-one function. The value of k for which area is minimum is 1.
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionLet f(x) be continuous function given by f(x)={2x,|x|≤1x2+ax+b,|x|>1}. Find the area of the region in the third quadrant bounded by the curves x=−2y2andy=f(x) lying on the left of the line 8x+1=0.
View SolutionLet f(x)= maximum {x^(2),(1-x)^(2),2x(1-x)} where0<=x<=1 The area of the region bounded by the curves y=f(x), x-axes,x=0 and x=1 is
View SolutionLet f(x) be continuous function such that f(0)=1,f(x)-f((x)/(7))=(x)/(7)AA x in R. The area bounded by the curve y=f(x) and the coordinate axes is
View SolutionLet f(x)={xifx≥1x2ifx<1 is f a continuous function ? Why ?
View SolutionLet f(x) be a continuous function such that the area bounded by the curve y=f(x), the x-axis, and the lines x=0 and x=ais1+a22sin a. Then,
View SolutionThe area of the region bounded by the function f(x)=x3 , the x-axis and the lines x=−1 and x = 1 is equal to
View SolutionLet f:[−1,2]→[0,∞) be a continuous function such that f(x)=f(1−x),∀x∈[−1,2]. If R1=∫2−1xf(x)dx and R2 are the area of the region bounded by y=f(x),x=−1,x=2 and the X-axis. Then :
View SolutionLet x≠0,|x|<12 and f(x)=1+2x+4x2+8x3+…… then , f−1(x)=
View Solutionमाना f(x) संतत फलन है तथा f(x)={2x|x|≤1 के लिए x2+ax+b|x|>1 के लिए है | तृतीय चतुर्थांश में वक्र x=-2y2 तथा y=f(x) के द्वारा परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए , जो कि रेखा 8x+1=0 के बायीं ओर स्थित है |
View SolutionLet f:[-1,2] to [0 , oo ) be a continuous function such that f(x)=f(1-x) for all x in [-1,2]. Let R_1= int_(-1)^2 x f(x) dx and R_2 be the area of the region bounded by the y=f(x), x=-1 , x=2 and the x-axis .Then :
View SolutionLet f(x) be continuous function given by f(x)={2x,|x|≤1and x2+ax+b,|x|>1}.
Find the area of the region in the third quadrant bounded by the curves x=−2y2andy=f(x) lying on the left of the line 8x+1=0.
View Solution
