Let . Draw the graph of the function and find the following
(a) Range of the function
(b) Point of inflection
(c) Point of local minimaSolution in Bengali
We have
which is a parabola having vertex at .
For when x = 0 and y = -1 when .
For y = -1 - cos x, y = -1 when and y = 0 when .
Hence the graph of the function y = f(x) is as shown in the following figure.
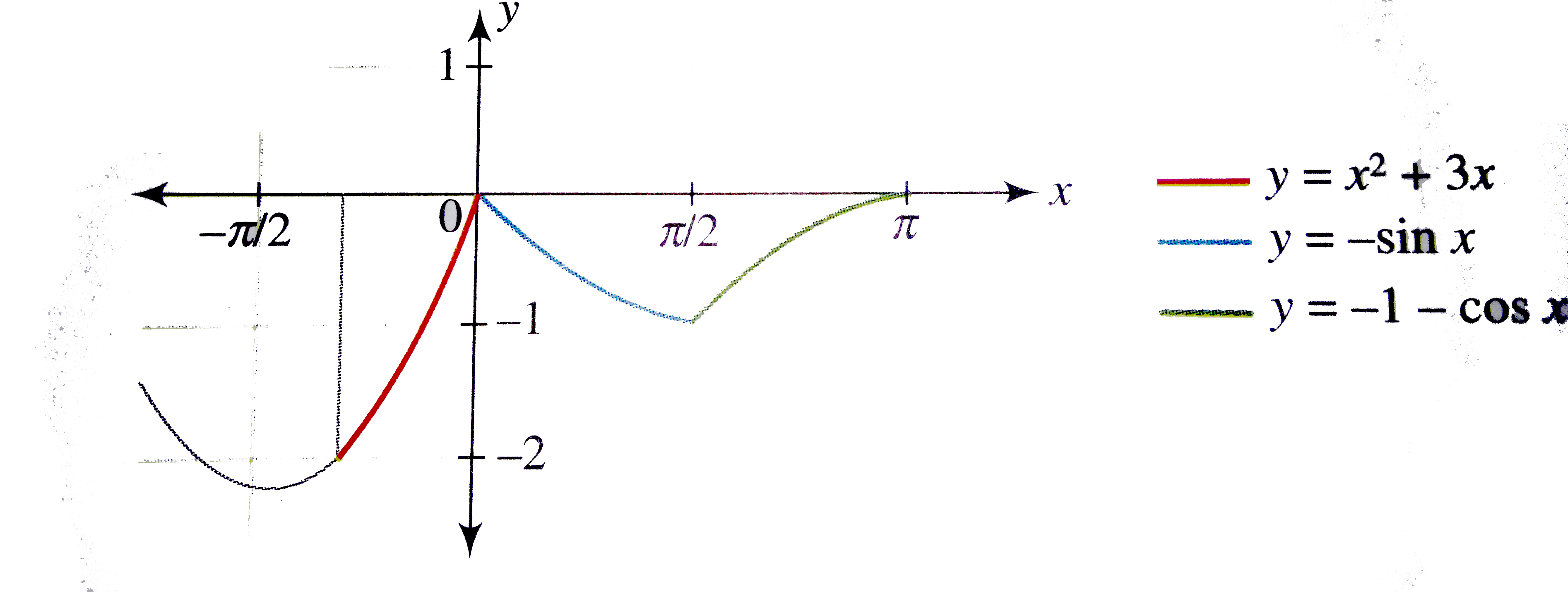
From the graph, is the point of local minima.
for for . SO the curve is concave upwards.
For for . So the curve is concave downwards.
Hence is the point of inflection.
The least value of occurs for , when x = -1.
Hence the least value is -2. Therefore, the range is [-2, 0].
Topper's Solved these Questions
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises
22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES
34 Videos
- HIGHT AND DISTANCE BOOK - CENGAGE PUBLICATIONCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives
3 Videos
Similar Questions
Draw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionDraw the graph of y=1(1/x).
View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
View SolutionLet f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩x2+3x,−1≤x<0−sinx,0≤x<π/2−1−cosx,π2≤x≤π . Draw the graph of the function and find the following
(a) Range of the function
(b) Point of inflection
(c) Point of local minima
View SolutionIf f(x)=⎧⎪ ⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪ ⎪⎩−x−π2 , x≤−π2−cosx , −π2<x≤0,thenx−1, 0<x≤1lnx, x>1
View Solutionयदि f(x)={(−x−π2,,x≤−π2),(−cosx,,−π2<x≤0,),(x−1,0<x≤1) तब-
View SolutionLet f(x)=⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩−2sinxfor−π≤x≤−π2asinx+bfor−π2<x<π2cosxforπ2≤x≤π. If f is continuous on [−π,π), then find the values of a and b.
View SolutionLet f(x) = ⎧⎪⎨⎪⎩x3+x2−10x−1≤x<0sinx0≤x<x/21+cosxπ/2≤x≤π then f(x) has
View SolutionLet f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩x3+x2−10x−1≤x<0cosx0≤x<π21+sinxπ2≤x≤x Then at x=π2, f(x) has:
View SolutionIf f(x) = {{:(-x - (pi)/(2),x le - (pi)/(2)),(-cos x,-(pi)/(2) lt x le 0),(x - 1,0 lt x le 1),(log x,x gt 1):} , Then
View SolutionLet f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩x2+3x,−1≤x<0−sinx,0≤x<π/2−1−cosx,π2≤x≤π . Draw the graph of the function and find the following
(a) Range of the function
(b) Point of inflection
(c) Point of local minima
View Solutionमाना फलन f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩sgn(x)+x−∞<x<0−1+sinx0≤x<π2cosxπ2≤x<∞ है। बिंदु x=0 तथा x=π2 पर संततता तथा अवकलनीयता की जाँच कीजिये।
View SolutionIf f(x)= {(-x-(pi)/(2)",",x le -(pi)/(2)),(-cos x,-(pi)/(2) lt x le 0),(x-1,0 lt x le 1),(ln x,x gt 1):} Then
View Solutionf(x)=⎧⎪ ⎪⎨⎪ ⎪⎩x+a√2sinx if 0≤x<π/42xcotx+b if π/4≤x≤π/2acos2x−bsinx if π/2<x≤π
f(x) is continuous on [0, π ] then (a,b) =
View SolutionLet f(x)=⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩−2sinxfor−π≤x≤−π2asinx+bfor−π2<x<π2cosxforπ2≤x≤π.
If f is continuous on [−π,π), then find the values of a and b.
View Solution
