Let f(x)=√|x|−{x}, where {.} denotes the fractional part of x an X,Y and its domain and range respectively, then
A
x∈(−∞,12] and Y∈[12,∞)
B
x∈(−∞,−12]∪[0,∞) and Y∈[12,∞)
C
X∈(−∞,−12]∪[0,∞) and Y∈[0,∞)
D
None of these
Video Solution
Text Solution
The correct Answer is:C
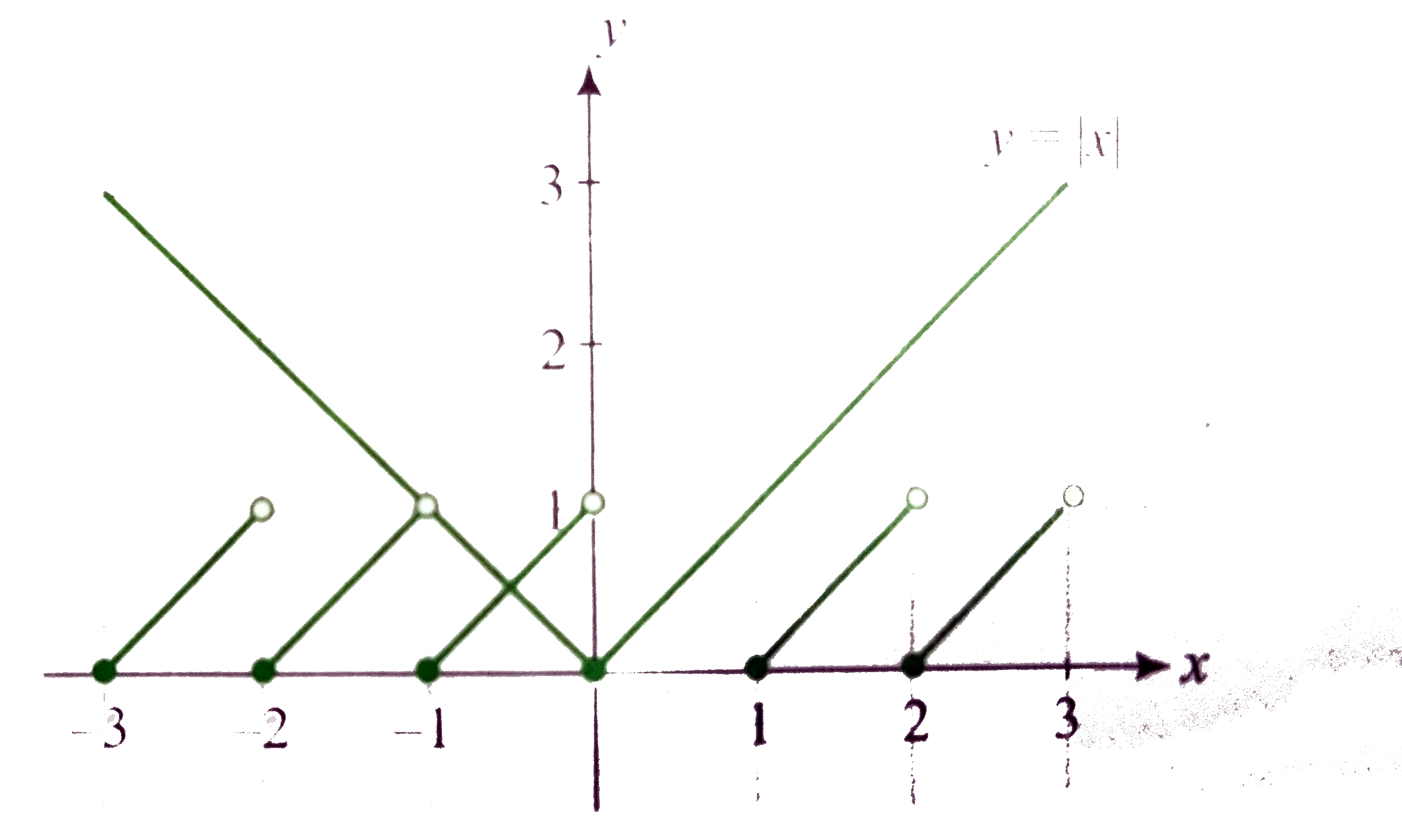
f(x)=√|x|−{x} is defined if |x|≥{x}
or x∈(−∞−12]∪[0,∞) or Y∈[0,∞).
|
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Multiple)
27 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Comprehension)
32 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise 1.15
8 Videos
- Quadratic Equations, Inequalities, Modulus and LogarithmsBOOK - CENGAGECHAPTER - Quadratic Equations, Inequalities, Modulus and LogarithmsEXERCISE - Question Bank
31 Videos
- SCALER TRIPLE PRODUCTS BOOK - CENGAGECHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.3
11 Videos
Similar Questions
Knowledge Check
if f(x)={x2}, where {x} denotes the fractional part of x , then
Af(X) is continuous at x=-2 but not at x=2Bf(x) is continuous at x=2 but not at x=-2Cf(x) is continuous at x=2 and x=-2Df(x) is discontinuous at x=-2 and at x=2(lim)x→11√|x|−{−x}(where{x} denotes the fractional part of (x) is equal to does not exist (b) 1 ∞ (d) 12
A16B24C32D8The range of f(x)=sin(sin−1{x}). where { ·} denotes the fractional part of x, is
A[0,1)B[0,1]C(-1,1)Dnone of these
Find the domain of f(x)=√|x|−{x} (where {⋅} denots the fractional part of x).
View SolutionIf f(x)−{x2}−({x})2,where (x) denotes the fractional part of x, then
View SolutionFor the function f(x)={x}, where {.} denotes the fractional part of x, x=1 is a point of
View SolutionThe domain of f(x)=1√−x2+{x} ; (where {.} denotes fractional part of x) is
View SolutionThe domain of f(x)=√2{x}2−3{x}+1 where {.} denotes the fractional part in [-1,1]
View Solution
