Let f(x)=[x]= Greatest integer less than or equal to x and k be an integer. Then, which one of the following in not correct?
A
limx→k−f(x)=k−1
B
limx→kf(x)=k
C
limx→kf(x)exists
D
limx→kf(x) does not exist
Text Solution
The correct Answer is:C
We have, f(x)=[x]
∴(LHS atx=k)
=limx→k−f(x)=limh→0=limh→0f(k−h)=limh→0[h−k]
=limh→0k−1=k−1[∵k−1<k−h<k−h<k∴[k−h]=k−1]
∴(RHLatx=k)
=limx→0f(x)=limh→0f(k−h)=limh→0[k+h]
=limh→0k=k[∵k<k+h<k+1∴[k+h]=k]
Clearly, limxt0k+f(x)≠limx→k+f(x).So,limx→kf(x) does not exist.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMACHAPTER - LIMITSEXERCISE - Section I - Solved Mcqs101videos
LIMITS
- BOOK - OBJECTIVE RD SHARMACHAPTER - LIMITSEXERCISE - Section II - Assertion Reason Type5videos
LIMITS
- BOOK - OBJECTIVE RD SHARMACHAPTER - INVERSE TRIGONOMETRIC FUNCTIONS EXERCISE - Chapter Test30videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - MATHEMATICAL INDUCTION EXERCISE - Exercise30videos
MATHEMATICAL INDUCTION
Similar Questions
Knowledge Check
- Question 1 - Select One
Let [x] be the greatest integer less than or equal to x, for a real number x. Then the following sum
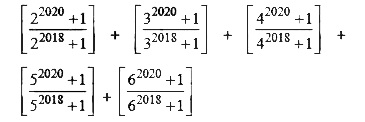
is-A80B85C90D95 - Question 2 - Select One
Let [x] denote the greatest integer less than or equal to x. Then, ∫−11[x]dx=?
A−1B0C12D2 - Question 3 - Select One
If the sum of the greatest integer less than or equal to x and the least integer than or equal to x is 5, then the solution set for x is
A[2,3]B(0,5)C[5,6)D[2,3)
Let [x] denotes the greatest integer less than or equal to x and f(x)=[tan2x]. Then
View SolutionIf f(x)=|x−1|−[x] (where [x] is greatest integer less than or equal to x) then.
View SolutionIf [x]represents the greatest integer less than or equal to x, then which of the following statement is ture
View SolutionLet f(x)={x}= greater integer less than or eqal to x. For any integer k, show that limx→kf(x) does not exist.
View SolutionIf the sum of the greatest integer less than or equal to x and the least integer than or equal to x is 5, then the solution set for x is
View Solution

