Let g(x)=√x−2k,∀2k≤x<2(k+1), where k∈ integer. Check whether g(x) is periodic or not.Solution in Bengali
g(x)=√x−2k,∀2k≤x<2(k+1), where k∈Z.
=⎧⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪⎩......√x+2,−2≤x<0√x,0≤x<2√x−2,2≤x<4√x−44≤x<6......
Graph of the function is as shown in the figure.
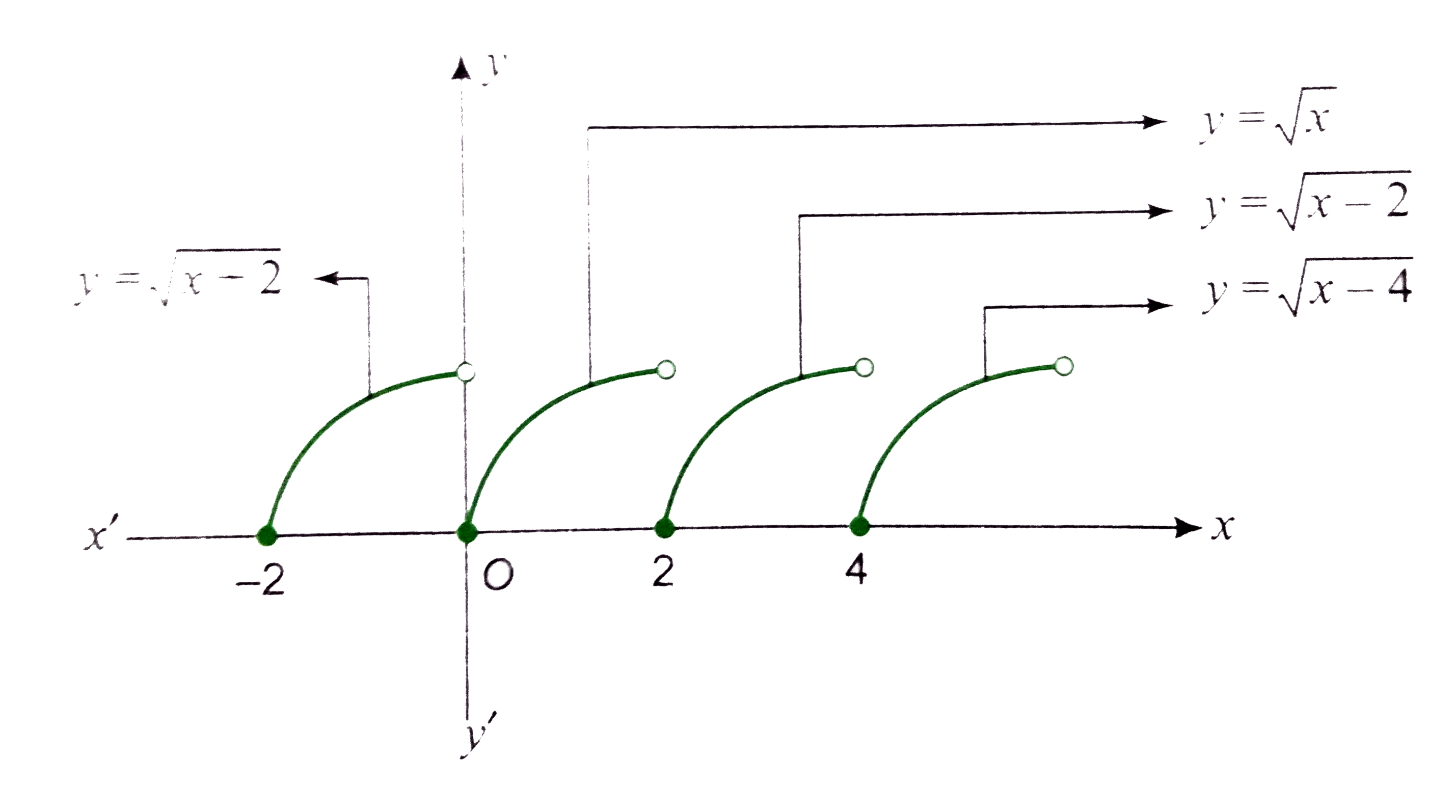
Topper's Solved these Questions
Similar Questions
Let ABCandABC' be two non-congruent triangles with sides AB=4,AC=AC′=2√2 and angle B=300 . The absolute value of the difference between the areas of these triangles is
04:38View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj−ˆk and ˆi−ˆj+ˆk, in the order form right-handed system ∀x ∈R, is
(a) 0 (b) 2 (c) 4 (d) 604:04View SolutionLet g(x)=√x−2k,∀2k≤x<2(k+1), where k∈ integer. Check whether g(x) is periodic or not.
04:21View Solutionf(x)=(cos^(2)x)/(1+cos x+cos^(2)x) and g(x)=k tan x+(1-k)sin x-x, where k in R,g'(x)=
02:14View SolutionLet f(x)=(log x)/(x), and solution of f(x)=k be denoted by g(k). {where k<0}g:(-oo,0)rarr(0,1), then y=g(x) will be
01:35View SolutionLet a function f be even and integrable everywhere and periodic with period 2. Let g(x)=∫x0f(t)dt and g(t)=kThe value of g(2) in terms of k is equal to (A) k (B) 2k (C) 3k (D) 5k
02:52View SolutionCheck whether following pairs of function are identical or not?
f(x)=√x2 and g(x)=(√x)2View SolutionLet g(x)=√x−2k,∀2k≤x<2(k+1) where, k∈l , then
04:40View SolutionColumn -1( Reaction Equilibrium ) Column -II ( Degree of dissociation of X in terms of their equilibrium constants assuming degree of dissociation of Y is same that of X whenever applicable ) ( P ) X ( g) rarr Z (g) + Y ( s) ( 1) ( 2 sqrt( K))/( 1+ 2 sqrt(K)) ( Q ) 2X(g) rarr Y (g) + Z ( g) ( 2) ( 2 sqrt( K))/( 1+ sqrt(K)) ( R ) X ( g) +Y(g) rarr Z(g) + W(g) ( 3) ( K )/( K +1) ( S ) X ( g) rarr ( Y )/( 2)(s) + ( Z)/( 2) (g) ( 4) ( 2K)/( 1+ 2K) Codes :
03:55View Solutionϕ(x)=f(x)⋅g(x)andf'(x)⋅g'(x)=k ,then 2kf(x)⋅g(x)=
04:52View SolutionLet g be a function defined by g(x)=√{x}+√1−{x} .where {.} is fractional part function, then g is
02:52View SolutionLet g(x)=√x−2k,∀2k≤x<2(k+1), where k∈ integer. Check whether g(x) is periodic or not.
05:02View SolutionLet g(x)=√x−2K,∀2K≤x<2(k+1), wherek∈ integer . If g(x) is periodic then period of g(x) is
02:48View Solutionϕ(x)=f(x)g(x)andf'(x)g'(x)=k, then 2kf(x)g(x) =
02:33View SolutionCheck whether following pairs of function are identical or not?
f(x)=√x2 and g(x)=(√x)201:16View SolutionLet a function f be even and integrable everywhere and periodic with period 2. Let g(x)=∫x0f(t)dt and g(t)=kThe value of g(2) in terms of k is equal to (A) k (B) 2k (C) 3k (D) 5k
04:14View Solution

