Let be an integer such that the triangle with vertices and has area units. Then the orthocentre of this triangle is at the point : (1) (2) (3) (4) Solution in Bengali
The correct Answer is:A
We have
or (no ral solution)
Since K is an integer,
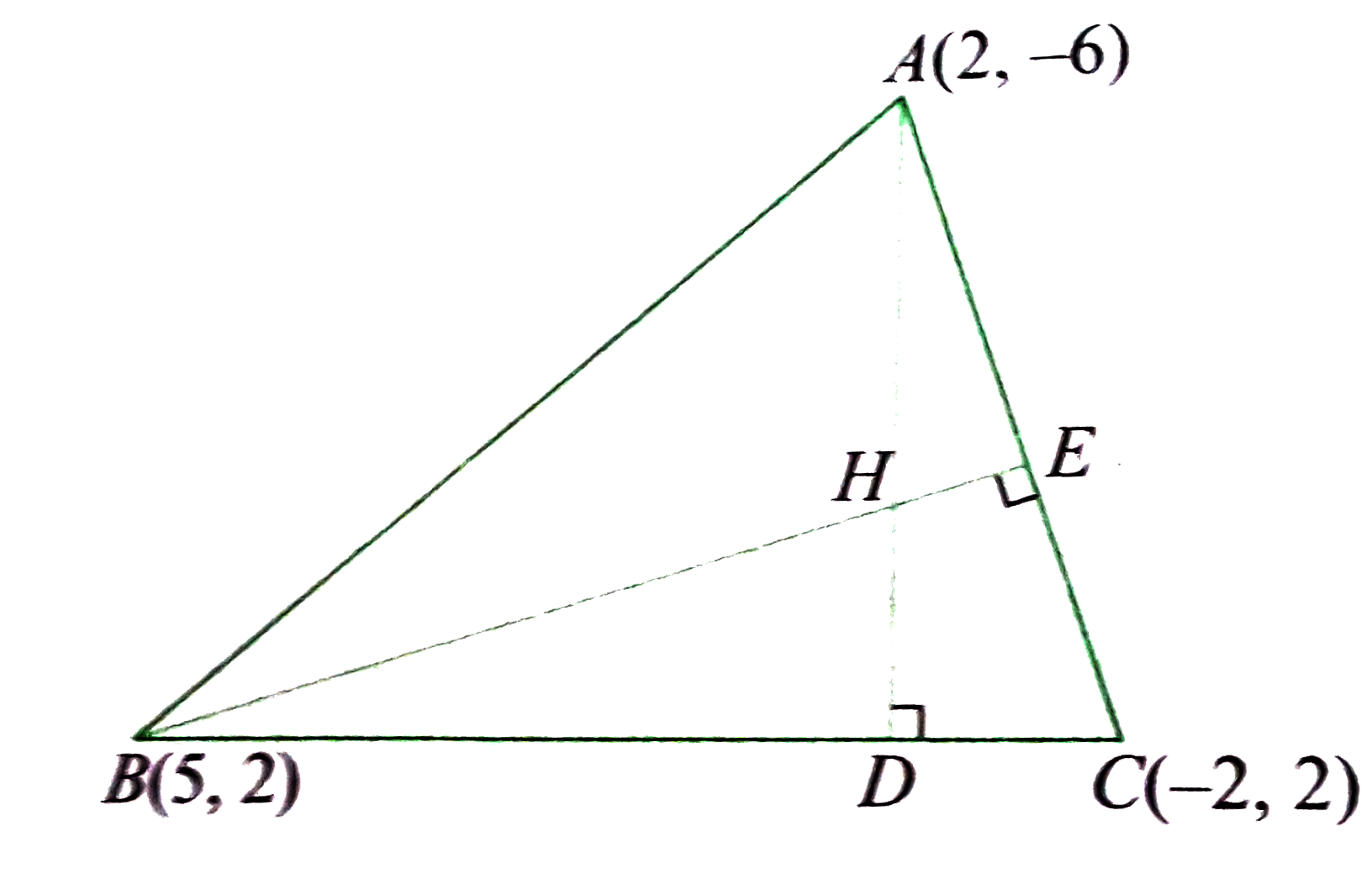
Form the figure, slope of BC is 0. So, equation of AD is
Slope of AC is .
Eqaution of line BE is
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Numerical value
12 Videos
- COORDINATE SYSTEMBOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGE PUBLICATIONCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
Line AB passes through point (2,3) and intersects the positive x and y-axes at A(a,0) and B(0,b) respectively. If the area of ΔAOB is 11. then the value of 4b2+9a2 is
View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
View SolutionIf the centroid of the triangle formed by the points (3, −5), (−7, 4), (10, −k) is at the point (k, −1) , then k= 3 (b) 1 (c) 2 (d) 4
View SolutionThe vertices of a triangle are (1, 2), (h, -3) and (-4, k). Find the value of √{(h+k)2+(h+3k)2}. If the centroid of the triangle be at point (5, -1).
View SolutionIf the centroid of the triangle whose vertices are (2, 4), (3, k) and (4, 2) is (k, 3) then k =
View Solutionयदि शीर्षों (2, -6), (5, 4) और (k, 4) वाले त्रिभुज का क्षेत्रफल 35 वर्ग एकक हो, तो k का मान है -
View Solutionमाना k एक ऐसा पूर्णाक है कि त्रिभुज, जिसके शीर्ष (k,−3k),(5,k) तथा (−k,2) है, का क्षेत्रफल 28 वर्ग इकाई है, तो त्रिभुज क लम्ब-केन्द्र जिस बिन्दु पर है, वह है
View Solutionমনে করো k একটি পূর্ণসংখ্যা। যদি (k, -3k), (5, k) এবং (-k, 2) বিন্দুত্রয় দ্বারা গঠিত ত্রিভুজের ক্ষেত্রফল 28 বর্গ একক হয়, তবে ত্রিভুজটির লম্ববিন্দুটি হবে—
View SolutionIf the area of a triangle with vertices (k, 2), (2, 4) and (3, 2) is 4 square units, find the value of k.
View Solutionमाना k एक ऐसा पूर्णांक हैं कि त्रिभुज, जिसके शीर्ष (k, - 3k) , (5,k) तथा (-k, 2) हैं, का क्षेत्रफल 28 वर्ग इकाई हैं, तो त्रिभुज का लम्ब-केन्द्र जिस बिन्दु पर हैं, वह हैं
View SolutionIf the area of the triangle with vertices at the points whose coordinates are (2, 5), (0, 3) and (4, k) is 4 units, then find the value of k.
View SolutionIf area of triangle is 35 sq. units with vertices (2, - 6), (5, 4) and (k, 4). Then k is :
View SolutionIf area of triangle is 35 sq. units with vertices (2,-6), (5, 4) and (k,4) then k is :
View SolutionIf (2,k,-1) is the centroid of the triangle with vertices (2,-1,2) (1,-3,-4) and (3,k,-1), then k=
View SolutionIf the vertices of a triangle are (2, 4), (5, k) and (3, 10) and its area is 15 sq. units, the value of k is
View Solution
