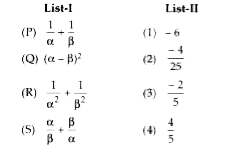let k>0,sα≡x2+y2+2αx+k=0 and sβ≡x2+y2+2βy−k=0 . Then match the items of List -I with those of List - II

The correct match is
A
A→(iii),B→(iv),C→(ii),D→(i)
B
A→(ii),B→(iv),C→(i),D→(iii)
C
A→(iv),B→(i),C→(iii),D→(ii)
D
A→(iv),B→(iii),C→(i),D→(ii)
Text Solution
The correct Answer is:C
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
If x2+α1x+β1=0 and x2+α2x+β2=0 have a common root (x−k), then find k.
Ak=α2−α1β2−β1Bk=α2−α1β2−β1Ck=α2−α1β2−β1Dk=α2−α1β2−β1Consider the system of equations :
x + y + z = 0
αx+βy+γz=0
α2x+β2y+γ2z=0
then the system of equations hasAa unique solution for all values of α,β,γBinfinite number of solutions if any two of α,β,γ are equalCa unique solution if α,β,γ are distinctDmore than one,but finite number of solutions depending on values of α,β,γIf α,β are the zeros of kx2−2x+3k such that α+β=αβ then k=?
A13B−13C23D−23
Let α,βandγ be real numbers. Consider the following system of linear equations
x+2y+z=7
x+αz=11
2x−3y+βz=γ
Match each entry in List-I to the correct entries in List-II.

The correct option is:
View SolutionIf α,β are the roots of ax2+bx+c=0 and k∈R then the condition so that α<k<β is :
View SolutionIf x2−2cosαx+1=0 and y2−2cosαy+1=0 then 2cos(α+β)=
View SolutionSuppose α,β are roots of x2−2x+4=0 If α4+β4=k , then |k| is equal to ______
View SolutionLet x and y be positive real numbers such that y3+y≤x−x3 . Then match the following list -I with List- II Where [.] is greatest integer function.
List - I List - II(P)[x1x−y1y](1)−1(Q)[x1x−1](2) 0(R) [3−(1−x)2](3) 1(s) [x2−y2+1](4)2
View Solution