Let n≥3 and let C1,C2,....,Cn be circles witht radii, r1,.r2,....,rn, respectively. Assume that C1andCi+1 touch external for 2≤i≤n−1. It is also given that the x-axis and the line y=2√2x+10 are tangential to each of the ci rcles. Then r1,r2,....,rn, are in-
ana arithmetic progeression with common difference 3+√3
a geometric progeression with common ratio 3+√3
an arithmetic progeression with common difference 2+√3
a geometric progeression with common ratio 2+√3
The correct Answer is:D
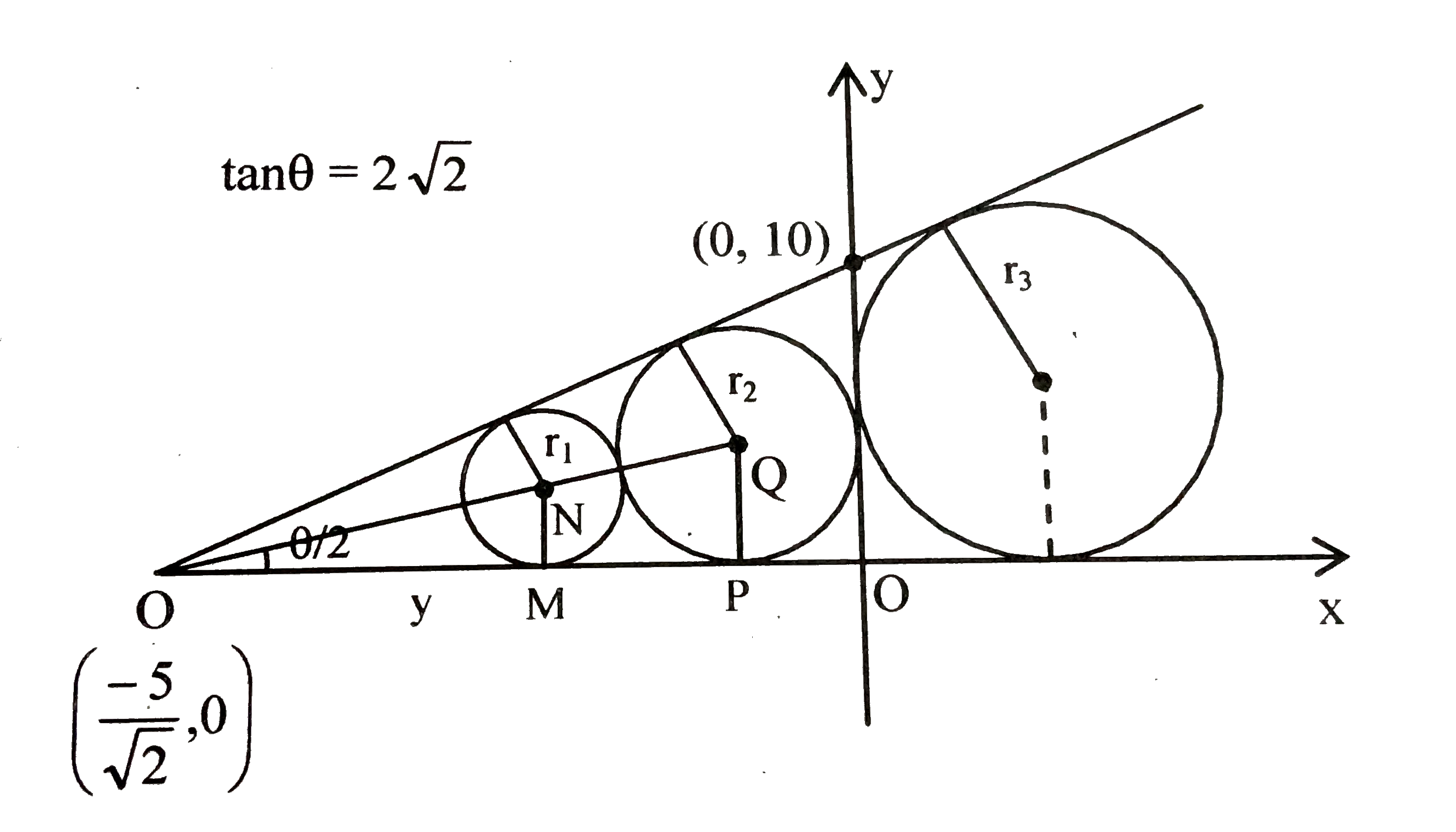
(−5√2,0)
tanθ=2−tanθ/21−tan2θ/2
2√2=2−tanθ/21−tan2θ/2
√2tan2θ/2+tanθ−√2=0
tanθ/2=−1±√1+82√2
=−1±32√2=1√2or−√2
∴tanθ/2=1√2 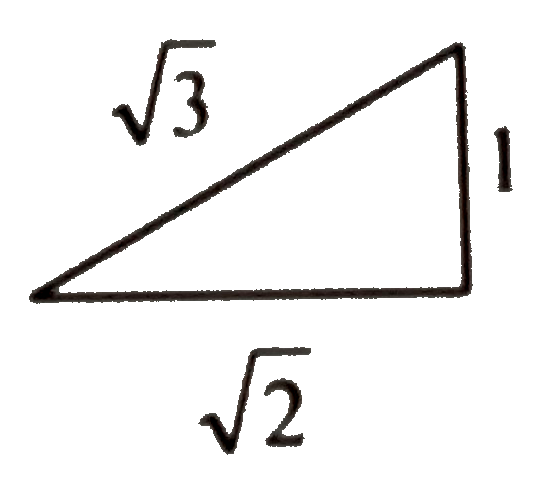
InΔOMNsinθ/2=r1ONsinθ/2=1√2
ON=√3r1
In ΔOMNsinθ/2=r1ON+r1+r2⇒1√3=r2√3r1+r1+r2
√3r1+r1+r2=√3r2
r1(√3+1)=r2(√3−1)
r2r1=√3+1√3−1
=(√3+1)22=2+√3
Topper's Solved these Questions
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - Part A - Mathematics
20 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - Part B- Mathematics
10 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - PART -I MATHEMATICS
20 Videos
- KVPY 2021BOOK - KVPY PREVIOUS YEARCHAPTER - KVPY 2021EXERCISE - PART II MATHEMATICS
4 Videos
Similar Questions
Let n≥3 and let C1,C2,....,Cn, be circles with radii r1,r2,...rn, respectively. Assume that Ci and Ci+1 touch externally for 1≤i≤n−1. It is also given that the x-axis and the line y=2√2x+10 are tangential to each of the circle . Then r1,r2.rn are in (A) an arithmetic progression with common difference 3+√2 (B) a geometric progression with common ratio 3+√2 (C) an arithmetic progression with common difference 2+√3 (D) a geometric progression with common ratio 2+√3
View SolutionThree circles with centres C1,C2andC3 and radii r1,r2andr3 where r1<r2<r3 are placed as shown in the figure
View Solution
Knowledge Check
Three circles C1,C2,C3 with radii r1,r2,r3(r1<r2<r3) respectively are given as r1=2, and r3=8 they are placed such that C2 lines to the right of C1 and touches it externally C3 lies ot the right of C2 and touches it externally. There exist two stratight lines each of whic is a direct common tangent simultaneously to all the three circles then r2 is equal to
Ar2=4Br2=5Cr2=10Dr2=16Given that C(n,r):C(n,r+1)=1:2andC(n,r+1):C(n,r+2)=2:3.
What is r equal to ?A2B3C4D5Given that C(n,r):C(n,r+1)=1:2andC(n,r+1):C(n,r+2)=2:3.
What is n equal to ?A11B12C13D14
Consider a series of 'n' concentric circles C1,C2,C3,.....,Cn with radii r1,r2,r3,......,rn respectively, satisfying r1>r2>r3....>rnandr1=10. The circles are such that the chord of contact of tangents from any point on C1 to Ci+1 is a tangent to Ci+2(i=1,2,3,...). Find the value of limn→∞n∑i=1r1, if the angle between the tangents from any point of C1 to C2 is π3.
View SolutionC1andC2 are fixed circles of radii r1andr2 touches each other externally. Circle 'C' touches both Circles C1andC2 extemelly. If r1r2=32 then the eccentricity of the locus of centre of circles C is
View SolutionProve that C(n,r)+C(n−1,r)+C(n−2,r)+.......+C(r,r)=C(n+1,r+1).
View SolutionLet r and n be positive integers such that 1≤r≤n. Then prove the following: n+n−1Cr−1=(n−r+1){}nCr−1
View SolutionnCr+1+nCr−1+2nCr=
View Solution
