Let be a point inside a triangle such that , then show that: Solution in Bengali
The correct Answer is:A

Applying sine rule in , we have
or ...(i)
Again in , we have
From Eqs. (i) and (ii), we have
or
or
Dividing both sides by , we get
or
Squaring both sides, we have
or
[since in ]
or
Area of triangle ABC,
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE PUBLICATIONCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Matrix match type
6 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE PUBLICATIONCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Numerical value type
22 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE PUBLICATIONCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Multiple correct answer type
24 Videos
- PROGRESSION AND SERIESBOOK - CENGAGE PUBLICATIONCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE )
8 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - All Questions
1119 Videos
Similar Questions
show that tan−1(12)+tan−1(211)=tan−1(34)
View SolutionSuppose α,β,γandδ are the interior angles of regular pentagon, hexagon, decagon, and dodecagon, respectively, then the value of |cosαsecβcosγcosecδ| is _________
View SolutionThe sides of ABC satisfy the equation 2a2+4b2+c2=4ab+2ac Then a) the triangle is isosceles b) the triangle is obtuse c) B=cos−1(78) d) A=cos−1(14)
View SolutionLet Sk,k=1,2,….100 denote the sum of the infinite geometric series whose first term is k−1K! and the common
ration is 1k then the value of (100)2100!+Σ100k=1|(k^2-3k+1)S_k| is ____________
View SolutionIf the function f:[1,∞)→[1,∞) is defined by f(x)=2x(x−1), then find f−1(x)
View SolutionIn figure, ΔODCΔOBA,∠BOC=125oand ∠CDO=70o. Find∠DOC,∠DCOand∠OAB.
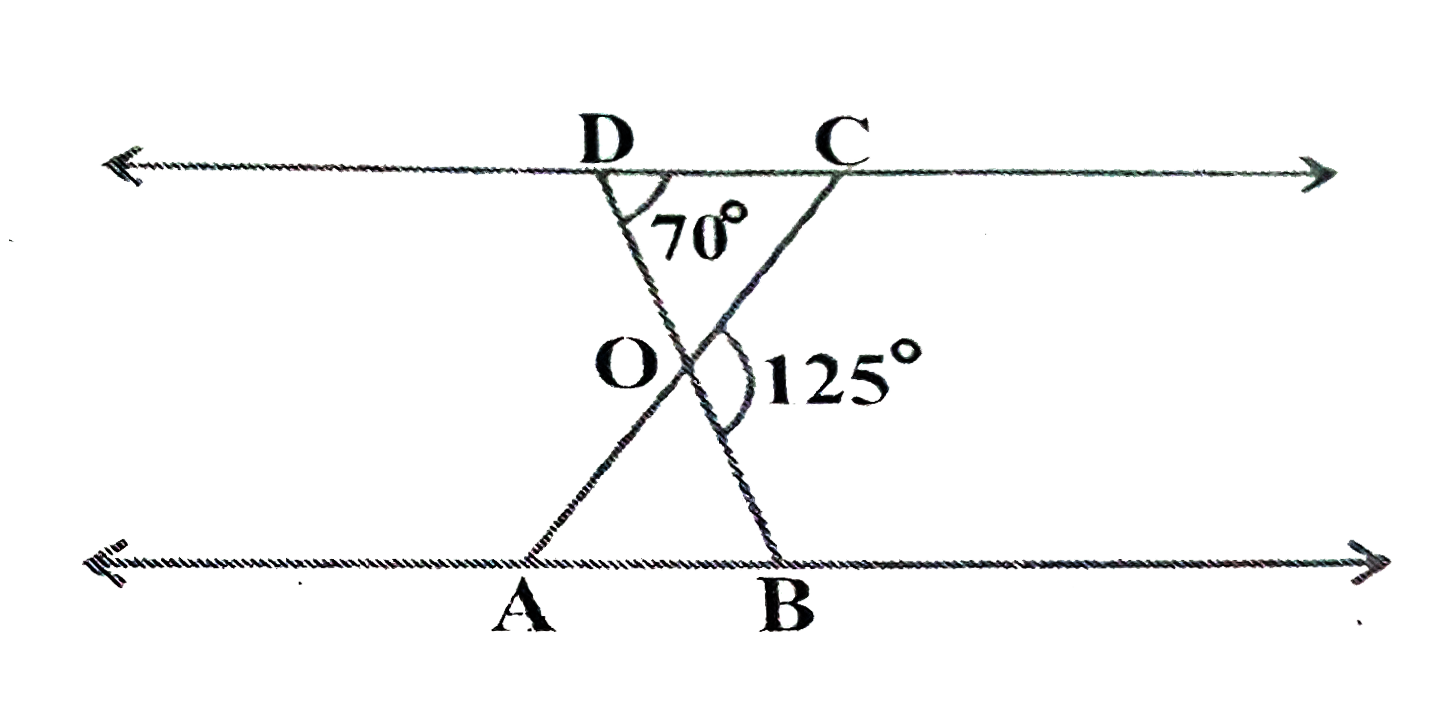
View SolutionThe diagonals of a rectangle ABCD meet at O . If ∠BOC=44∘, find ∠OAD
View Solutionयदि A+B+C=π हो तो सिद्ध कीजिए कि -
(cotB+cotC)(cotC+cotA)(cotA+cotB)=cosec A cosec B cosec C.
View SolutionIn figure, ΔODC~ΔOBA,∠BOC=125oand ∠CDO=70o. Find∠DOC,∠DCOand∠OAB.
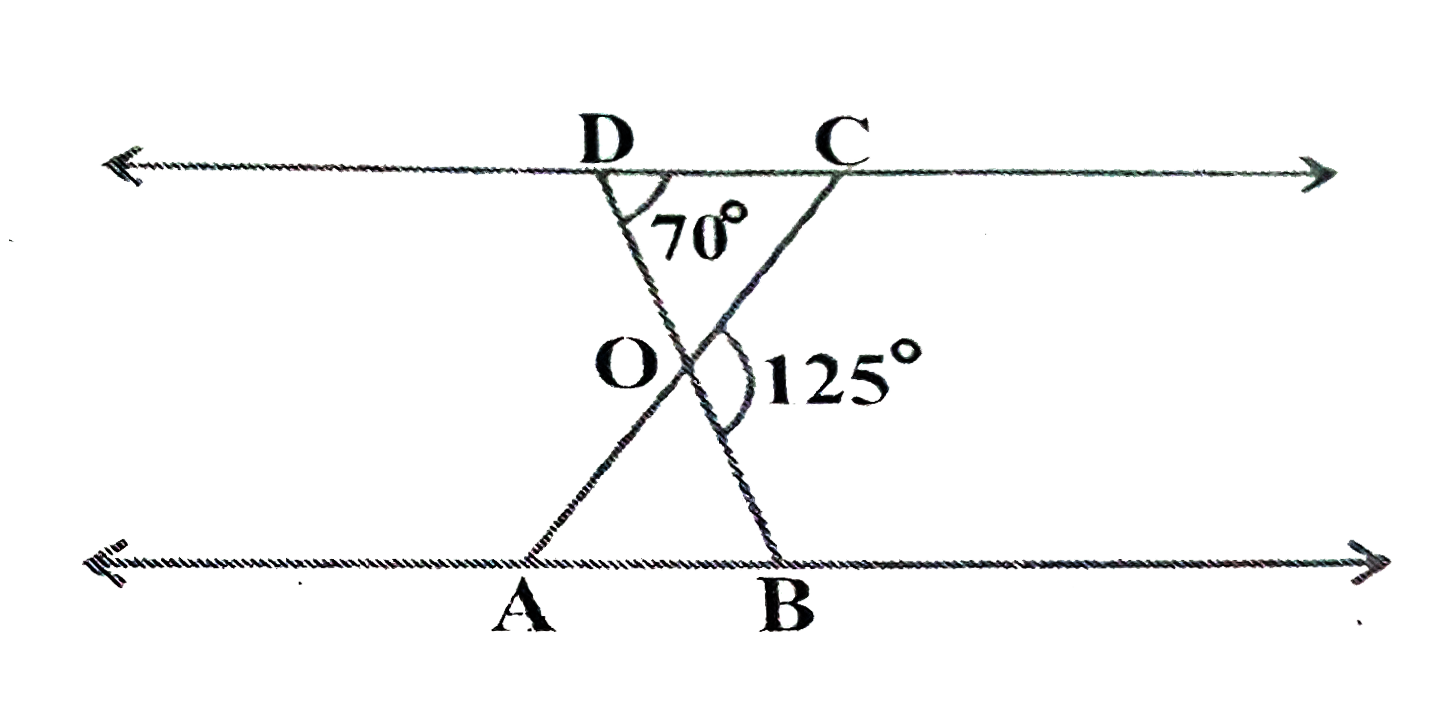
View SolutionLet O be a point inside a triangle ABC such that ∠OAB=∠OBC=∠OCA=ω , then show that: cotω=cotA+cotB+cotC Cosec2ω=cosec2A+cosec2B+cosec2C
View SolutionThe diagonals of a rectangle ABCD meet at O. If ∠BOC=440, find ∠OAD.
View SolutionThe diagonals of a rectangle ABCD meet at O . If ∠BOC=440, find ∠OAD
View SolutionAB and CD are diameters of a circle with centre O. If ∠OBD=500, find ∠AOC
View SolutionIf O is the circumcentre of ABC, then find the value of ∠OBC+ ∠BAC
View SolutionIn Figure, ABCD is quadrilateral inscribed in a circle with centre O.CD is produced to E such that ∠ADE=950and ∠OBA=300. Find ∠OAC.
View SolutionThe diagonals of a rectangle ABCD meet at O. If ∠BOC=440, find ∠OAD.
View Solution
