Let O be an interior point of ΔABC such that ¯¯¯¯¯¯OA+2¯¯¯¯¯¯OB+3¯¯¯¯¯¯OC=0. Then the ratio of a ΔABC to area of ΔAOC is
2
32
3
52
The correct Answer is:C
To solve the problem, we need to find the ratio of the area of triangle ABC to the area of triangle AOC given that →OA+2→OB+3→OC=0.
1. Understanding the Given Equation:
We have the equation →OA+2→OB+3→OC=0. This implies that we can express →OA in terms of →OB and →OC:
→OA=−2→OB−3→OC
2. Setting Up the Area of Triangle ABC:
The area of triangle ABC can be expressed using the cross product:
AreaABC=12|→AB×→AC|
where →AB=→B−→A and →AC=→C−→A.
3. Expressing Vectors:
Substitute →A=→OA, →B=→OB, and →C=→OC:
→AB=→B−→A=→OB−→OA
→AC=→C−→A=→OC−→OA
4. Calculating Area of Triangle AOC:
The area of triangle AOC can also be expressed using the cross product:
AreaAOC=12|→OA×→OC|
5. Substituting for →OA:
Substitute →OA=−2→OB−3→OC into the area formula for triangle AOC:
AreaAOC=12|(−2→OB−3→OC)×→OC|
6. Using the Properties of Cross Product:
The cross product →OC×→OC=0, thus:
AreaAOC=12|(−2→OB)×→OC|
=12⋅2|→OB×→OC|=|→OB×→OC|
7. Finding the Ratio of Areas:
Now, we can find the ratio of the areas:
AreaABCAreaAOC=12|→AB×→AC||→OB×→OC|
8. Using the Relationship:
From the equation →OA+2→OB+3→OC=0, we can deduce that the coefficients (1, 2, 3) represent the relative areas of the triangles formed. Thus, the ratio of the area of triangle ABC to the area of triangle AOC is:
AreaABCAreaAOC=3
Final Answer:
The ratio of the area of triangle ABC to the area of triangle AOC is 3.
We have the equation →OA+2→OB+3→OC=0. This implies that we can express →OA in terms of →OB and →OC:
→OA=−2→OB−3→OC
The area of triangle ABC can be expressed using the cross product:
AreaABC=12|→AB×→AC|
where →AB=→B−→A and →AC=→C−→A.
Substitute →A=→OA, →B=→OB, and →C=→OC:
→AB=→B−→A=→OB−→OA
→AC=→C−→A=→OC−→OA
The area of triangle AOC can also be expressed using the cross product:
AreaAOC=12|→OA×→OC|
Substitute →OA=−2→OB−3→OC into the area formula for triangle AOC:
AreaAOC=12|(−2→OB−3→OC)×→OC|
The cross product →OC×→OC=0, thus:
AreaAOC=12|(−2→OB)×→OC|
=12⋅2|→OB×→OC|=|→OB×→OC|
Now, we can find the ratio of the areas:
AreaABCAreaAOC=12|→AB×→AC||→OB×→OC|
From the equation →OA+2→OB+3→OC=0, we can deduce that the coefficients (1, 2, 3) represent the relative areas of the triangles formed. Thus, the ratio of the area of triangle ABC to the area of triangle AOC is:
AreaABCAreaAOC=3
The ratio of the area of triangle ABC to the area of triangle AOC is 3.
Topper's Solved these Questions
Similar Questions
Let O be an interior point of triangle ABC, such that 2−−→OA+3−−→OB+4−−→OC=0, then the ratio of the area of ΔABC to the area of ΔAOC is
View SolutionLet O be any point in the interior of ΔABC, prove that :
AB+BC+CA<2(OA+OB+OC)
View SolutionIf ¯¯¯¯¯¯XY=3, what is the area of ΔXYZ ?
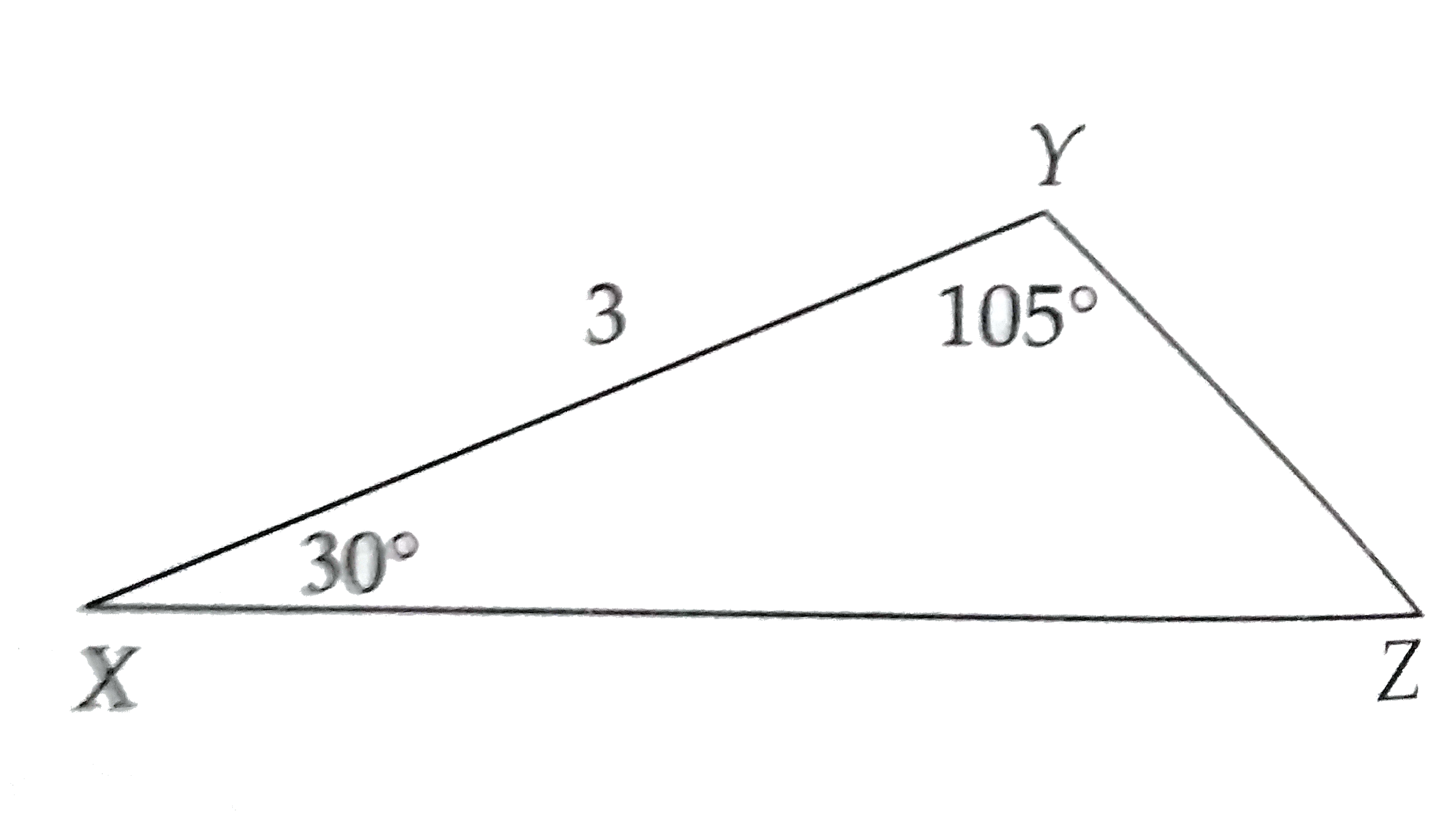
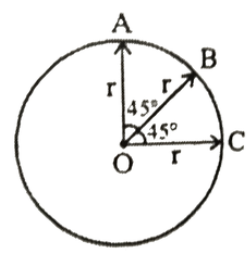
View SolutionThe resultant of the three vectors ¯¯¯¯¯¯OA,¯¯¯¯¯¯OB and ¯¯¯¯¯¯OC shown in figure :-
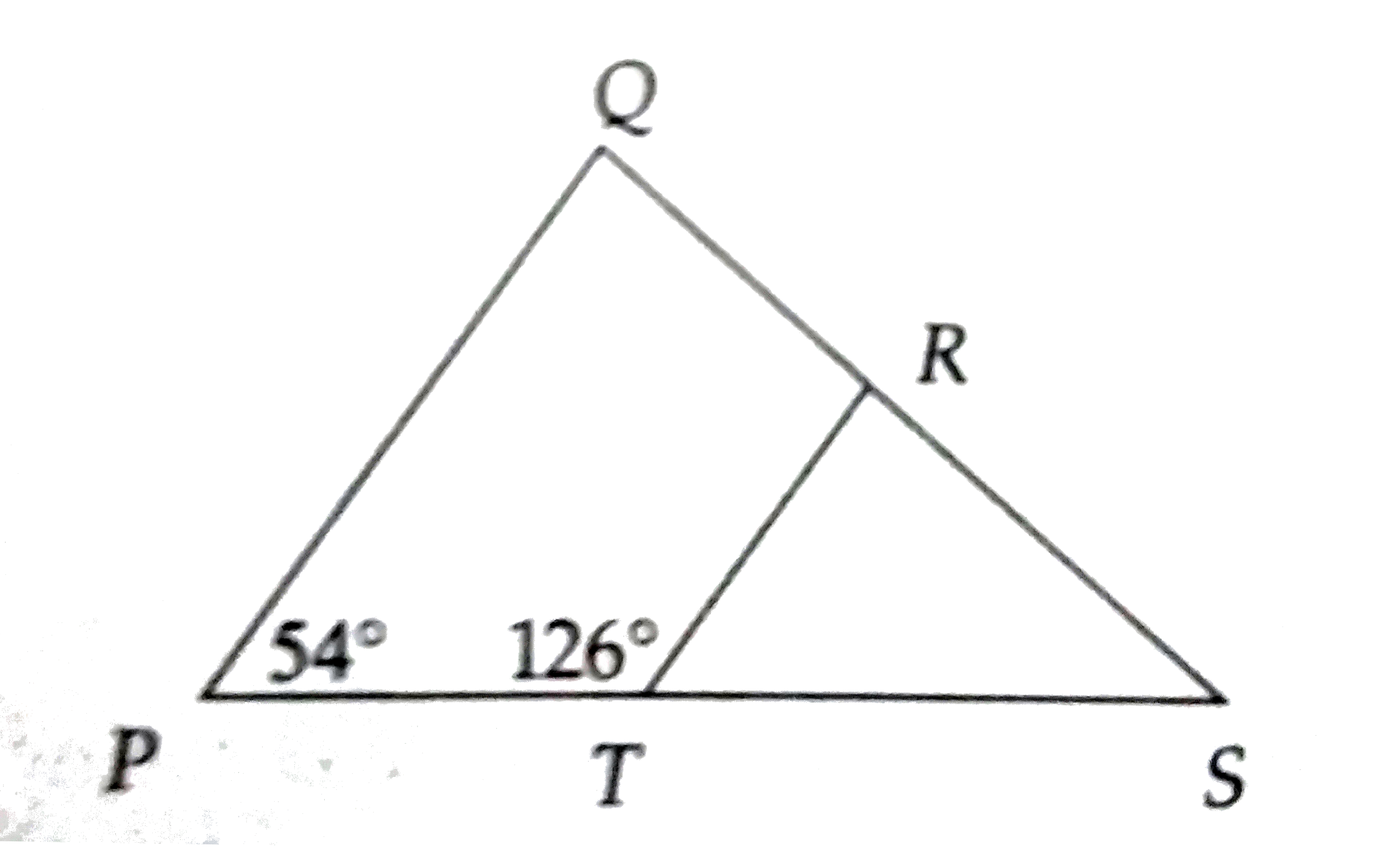
View Solution¯¯¯¯¯¯QR=¯¯¯¯¯RS. If the area of ΔRST is c2, what is the area of ΔQSP ?
View SolutionIn the given figure, D is the mid-point of BC, E is the mid-point of BD and O is the mid-point of AE. Find the ratio of area of ΔBOEandΔABC

View SolutionIf the ratio of angles of ΔABC is 1:2:3, find the ratio of its sides.
View SolutionGiven a cube ABCD A1B1C1D1 which lower base ABCD, upper base A1B1C1D1 and the lateral edges AA1,BB1,CC1 and DD1 M and M1 are the centres of the forces ABCD and A1B1C1D1 respectively. O is a point on the line MM2 such that ¯¯¯¯¯¯OA+¯¯¯¯¯¯OB,¯¯¯¯¯¯OC+¯¯¯¯¯¯OD=¯¯¯¯¯¯¯OM, then ¯¯¯¯¯¯¯OM=λ(OM1) is equal to
View SolutionEvaluate :
2.¯7+1.¯3
View Solution
In the figure above, the circle with center O has ¯¯¯¯¯¯PQ tangent to it at P. Find the ratio of the shaded area to the area of the circle .
View Solution
