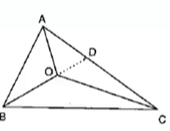
Let O be any point in the interior of ΔABC, prove that :
AB+BC+CA<2(OA+OB+OC)
Step by step video & image solution for Let O be any point in the interior of DeltaABC, prove that : AB+BC+CA lt 2 (OA+OB+OC) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
From a point O in the interior of a ΔABC perpendiculars OD, OE and OF are drawn to the sides BC, CA and AB respectively, then which one of the following is true ?
AAF2+BD2+CE2=AE2+CD2+BF2BAB2+BC2=AC2CAF2+BD2+CE2=OA2+OB2+OC2DAF2+BD2+CE2=OD2+OE2+OF2
If G be the centroid of the ΔABCandO be any other point in theplane of the triangle ABC, then prove that: OA2+OB2+OC2=GA2+GB2+GB2+GC2+3GO2
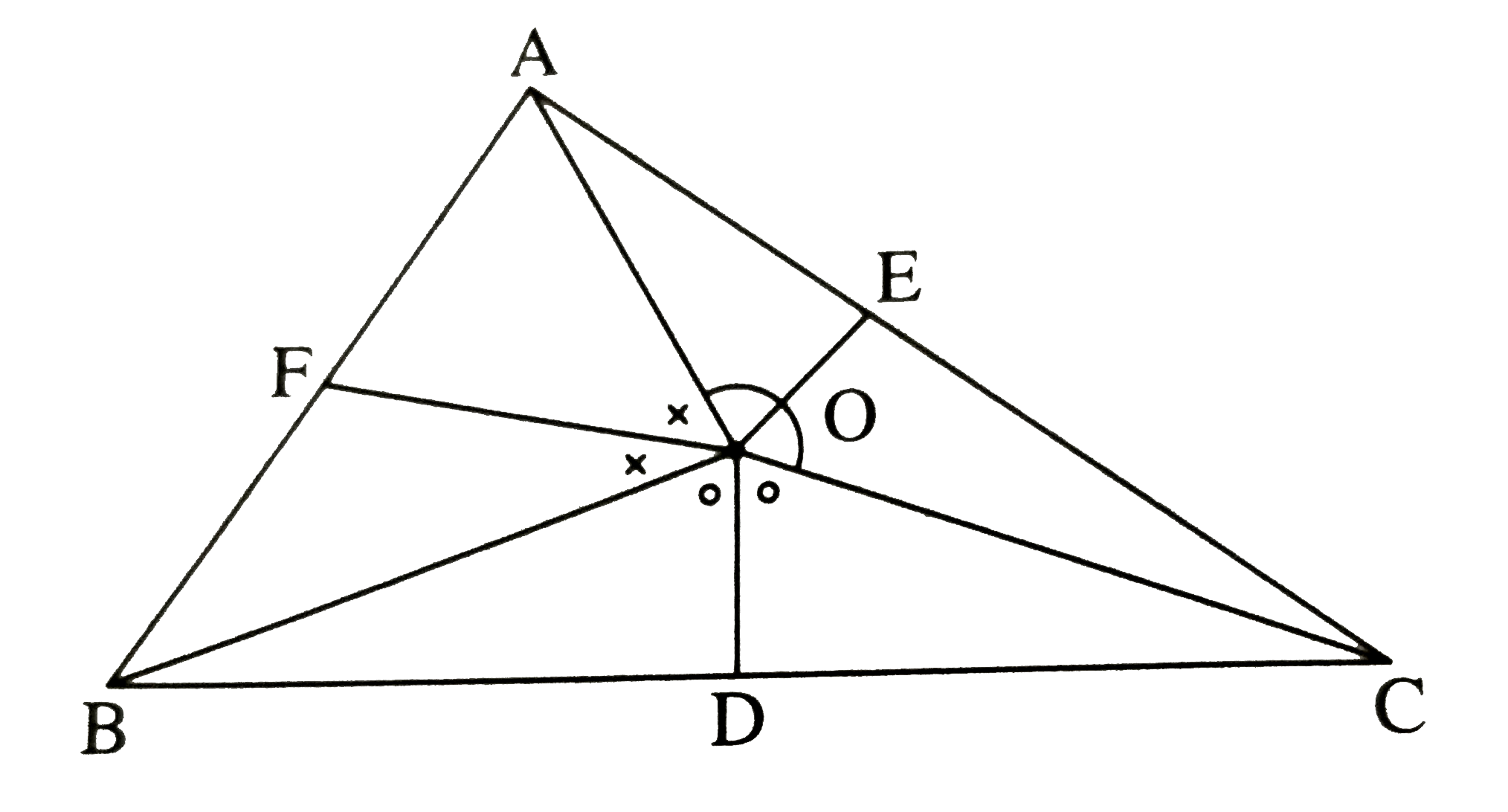
View SolutionO is any point in the interior of ΔABC. Bisectors of ∠AOB,BOC and AOC intersect sideAB, side BC, side AC in F,D and E respectively.
Prove that BF×AE×CD=AF×CE×BD.
 View Solution
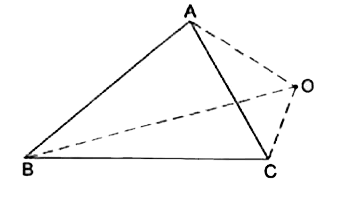
View SolutionIf O is point in the exterior of △ABC,show that 2(OA+OB+OC)>(AB+BC+CA)
 View Solution
View SolutionLet O be an interior point of ΔABC such that 2→OA+5→OB+10→OC=→0
View SolutionIf O is the circumcentre and P the orthocentre of ΔABC, prove that −−→OA+−−→OB+−−→OC=−−→OP.
View SolutionIn ΔABC,D is any point on side BC. Prove that
AB+BC+CA>2ADView SolutionIn ΔABC, if D is any point on the side BC, show that (AB+BC+AC)>2AD.
 View Solution
View Solution