Let O be the origin and let PQR be an arbitrary triangle. The point S is such that ¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OQ+¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OP+¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OR+¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OS Then the triangle PQR has S as itsSolution in Bengali
centriod
circumectre
incente
orthocenter
The correct Answer is:D
−−→OP.−−→OQ+−−→OR.−−→OS=−−→OR−−−→OP+−−→OQ.−−→OS.
=−−→OP.(−−→OQ−−−→OR)=−−→OS.(−−→OQ−−−→OR)
⇒(−−→OP−−−→OS).(−−→RQ)=0⇒−→SP.−−→RQ=0
⇒−→SP⊥−−→RQ
Similarly ,−−→SR⊥−−→OPand−−→SQ⊥−−→PR.
hence , S is orthocenter.
Topper's Solved these Questions
- JEE 2019BOOK - CENGAGE PUBLICATIONCHAPTER - JEE 2019EXERCISE - Linked comprehesion type
2 Videos
- JEE 2019BOOK - CENGAGE PUBLICATIONCHAPTER - JEE 2019EXERCISE - chapter -3
1 Videos
- JEE 2019BOOK - CENGAGE PUBLICATIONCHAPTER - JEE 2019EXERCISE - multiple correct answers type
1 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - All Questions
541 Videos
- LIMITSBOOK - CENGAGE PUBLICATIONCHAPTER - LIMITSEXERCISE - Comprehension Type
4 Videos
Similar Questions
Let O be the origin and−−→OX,−−→OY,−−→OZ be three unit vector in the directions of the sides −−→QR,−−→RP,−−→PQ respectively , of a triangle PQR.
∣∣∣−−→OX×−−→OY∣∣∣=
View SolutionThe equation of the plane passing through the point (1,1,1) and perpendicular to the planes 2x+y−2z=5and3x−6y−2z=7
View SolutionConsider a pyramid OPQRS located in the first octant (x≥0,y≥0,z≥0) with O as origin and OP and OR along the X-axis and the Y-axis , respectively. The base OPQRS of the pyramid is a square with OP=3. The point S is directly above the mid point T of diagonal OQ such that TS=3. Then,
View SolutionFind x satisfying [tanx]+[cotx]=2, where [.] represents the greatest integer function.
View Solutionlimx→0sin2xx
View SolutionIf bar(PO)+bar(OQ)=bar(QO)+bar(OR), then prove that the points P,Q and R are collinear.
View SolutionLet O be the origin and let PQR be an arbitrary triangle. The point S is such that bar(OP)*bar(OQ)+bar(OR)*bar(OS)=bar(OR)*bar(OP)+bar(OQ)*bar(OS)=bar(OQ)*bar(OR)+bar(OP)*bar(OS) Then the triangle PQR has S as its
View SolutionLet PQRS be a parallelogram whose diagonals PR and QS intersect at O'. IF O is the origin then : ¯¯¯¯¯¯OP+¯¯¯¯¯¯OQ+¯¯¯¯¯¯OR+¯¯¯¯¯¯OS=
View Solutionमाना कि O मुलबिन्दु है एवं PQR एक स्वेच्छिक त्रिभुज है | बिन्दु S इस प्रकार है कि
−−→OP.−−→OQ+−−→OR.−−→OS=−−→OR.−−→OP+−−→OQ.−−→OS=−−→OQ.−−→OR+−−→OP.−−→OS
तब बिन्दु S त्रिभुज PQR का है
View SolutionO is the origin , P(2,3,4), Q(1,k,1) are points such that ¯¯¯¯¯¯OP⊥¯¯¯¯¯¯OQ then find k.
View SolutionIn the following map bar OP, bar OQ, bar OR And bar OS S are 4 rays /_POQ +/_ QOR + /_SOR + /_POS =360^(0) Prove that.
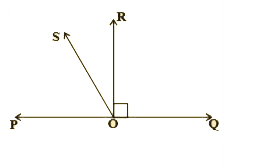
View SolutionIn the given figure ¯¯¯¯¯¯PQ is a line. Ray ¯¯¯¯¯¯OR is perpendicular to line ¯¯¯¯¯¯PQ.¯¯¯¯¯¯OS is another ray lying between rays ¯¯¯¯¯¯OPand ¯¯¯¯¯¯OR . Prove that ∠ROS=12∠QOS−∠POS
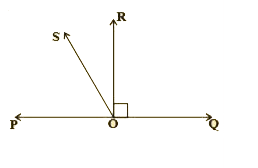
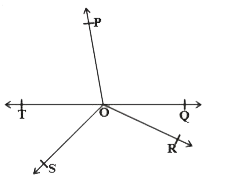
View SolutionIn the adjacent figure ¯¯¯¯¯¯OP,¯¯¯¯¯¯OQ,¯¯¯¯¯¯OR and¯¯¯¯¯¯OS are four rays. Prove that
∠POQ+∠QOR+∠SOR+∠POS=360∘ .
View SolutionIn the given figure ¯¯¯¯¯¯PQ is a line. Ray ¯¯¯¯¯¯OR is perpendicular to line ¯¯¯¯¯¯PQ.¯¯¯¯¯¯OS is another ray lying between rays ¯¯¯¯¯¯OPand ¯¯¯¯¯¯OR . Prove that ∠ROS=12∠QOS−∠POS
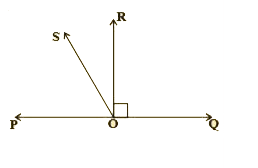
View SolutionIn the adjacent figure ¯¯¯¯¯¯OP,¯¯¯¯¯¯OQ,¯¯¯¯¯¯OR and¯¯¯¯¯¯OS are four rays. Prove that
∠POQ+∠QOR+∠SOR+∠POS=360∘ .
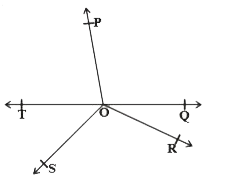
View SolutionIn the given figure ¯¯¯¯¯¯PQ is a line. Ray ¯¯¯¯¯¯OR is perpendicular to line ¯¯¯¯¯¯PQ.¯¯¯¯¯¯OS is another ray lying between rays ¯¯¯¯¯¯OPand ¯¯¯¯¯¯OR . Prove that ∠ROS=12∠QOS−∠POS
View Solution
