Let O(0,0),A(2,0),andB(11√3) be the vertices of a triangle. Let R be the region consisting of all those points P inside OAB which satisfy d(P,OA)≤min[d(p,OB),d(P,AB)] , where d denotes the distance from the point to the corresponding line. Sketch the region R and find its area.
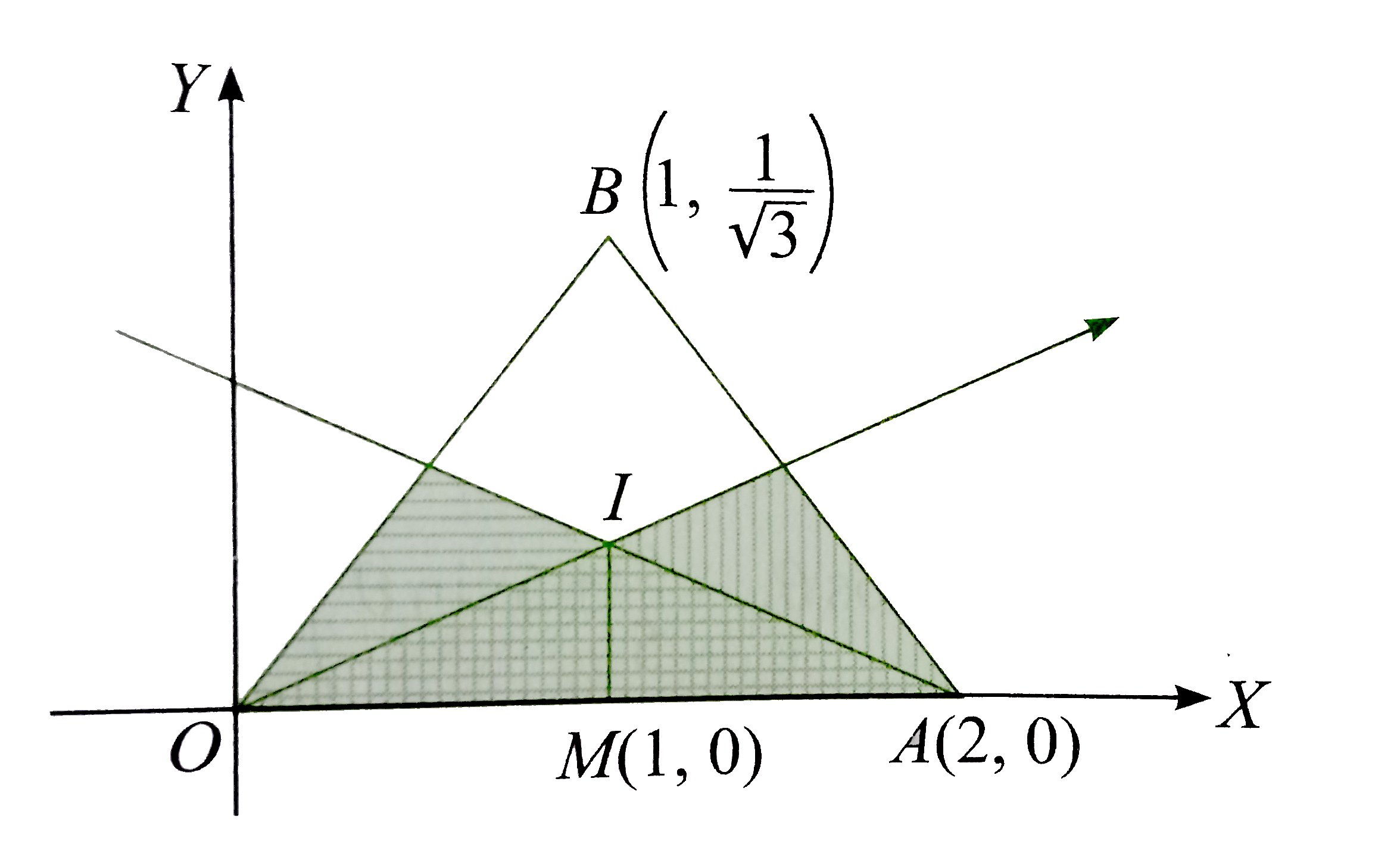
d(P,OA)≤ min[d(P,OB),d(P,AB)],
⇒d(P,OA)≤d(P,OB)and d(P,OA)≤d(P,AB),
When d(P,OA)= d(P,OB), P is equidistant from OA and OB, i.e., P lies on angle bisector of lines OA and OB.
So, when d(P,OA)<d(P,OB), Point P is nearer to OA than to OB, i.e., it lies below bisector of OA and oB.
Similarly, when d(P,OA)<d(P,AB) P is nearer to OA than to AB, i.e., it lies below bisector of OA and AB.
Common region satisfied by these two inequalities is the region formed by two bisectors and OA, i.e., triangle OIA.
∴ Required area = Area of triangle OIA
Now, ∠BOA=1/√31=1√3
∴∠BOA=30∘
⇒∠IOA=15∘
⇒IM=tan15∘=2−√3
∴Area of triangle OIA=12×OA×IM
=12×2×(2−√3)=2−√3 sq. units
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.123videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.24videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year9videos
THEORY OF EQUATIONS
Similar Questions
Let ABC be a triangle with vertices A≡(6,,2√3+1))),B≡(4,2)andC≡(8,2). Let R be the region consisting of all those points P inside ΔABC which satisfyd(P,BC)≥max{d(P,AB);d(P,AC)}, where d(P, L) denotes the distance of the point from the line L, then
View SolutionLet O(0.0),A(6,0) and B(3,√3) be the vertices of △OAB. Let R those points P inside △OAB which satisfy d(P, OA) minimum (d(P,OB),d(P,AB) where d(P, OA), d(P, OB) and d(P, AB) represent the distance of P from the sides OA, OB and AFB respectively. If the area of region R is 9(a−√b) where a and b are coprime, then find the value of (a+ b)
View Solution
Knowledge Check
- Question 1 - Select One
Let O(0, 0) and B(1,1√3) be the vertices of a triangle. Let R be the region consisting of all those points P inside ΔOAB satisfying. d(P,OA)lr min {d(P,OB),d(P,AB)}, where d denotes the distance from the point P to the corresponding line. Let M be peak of region R.
The perimeter of region R is equal toA√3B1√3C3D2−√3 - Question 2 - Select One
Let O(0,0),A(2,0)andB(1,1√3) be the vertices of a triangle. Let R be the region consisting of all those points P inside ΔOAB satisfying. d(P,OA)lr min {d(P,OB),d(P,AB)}, where d denotes the distance from the point P to the corresponding line. Let M be peak of region R. The perimeter of region R is equal to
A4−√3B4+√3C4+3√3D2+4√(2−√3) - Question 3 - Select One
Consider the traingle having vertices O(0,0),A(2,0), and B(1,√3). Also b≤min{a1,a2,a3....an} means b≤a1 when a1 is least, b≤a2 when a2 is least, and so on. Form this, we can say b≤a1,b≤a2,.....b≤an.
Let R be the region consisting of all those points P inside ΔOAB which satisfy d(P,OA)≤min[d(P,OB),d(P,AB)], where d denotes the distance from the point to the corresponding line. then the area of the region R isA√3sq,unitsB(2+√3) sq.unitsC√3/2 sq.unitsD1/√3 sq.units
Let O(0,0),A(2,0) be the vertices of an isosceles triangle inscribed in an ellipse (x−1)2+3y2=1. Let S represents the region consisting all those points P inside the given triangle which stales that, Distance of point P from OA is not more than the minimum distance of point p from the other two sides of the triangle".
View SolutionLet d(P,OA)≤min{d(P,AB),d(P,BC),d(P,OC)} where d denotes the distance from the point to the corresponding line and S be the region consisting of all those points P inside the rectangle OABC such that O=(0,0),A=(3,0),B=(3,2)andC=(0,2), which satisfy the above relation, then area of the region S is
View SolutionLet O(0, 0), P(3, 4), Q(6, 0) be the vertices of the triangle OPQ. The point R inside the triangle OPQ is such that the triangles OPR, PQR are of equal area. The coordinates of R are
View SolutionLet O(0,0),A(2,0),B(1,1√3) distance of P from the side OA is less than its distance from the syme vertices of a triangle. A point P moves inside the triangle such that the distance of P from the side OA is less than its distance from the sides OB and AB. The area traced by Pis
View SolutionTwo points O(0,0) and A(3,√3) with another point P form an equilateral triangle. Find the coordinates of P.
View Solution

