Let P be any point on a directrix of an ellipse of eccentricity e,S be the corresponding focus, and C the center of the ellipse. The line PC meets the ellipse at A. The angle between at A is α. Then α is equal to
tan−1e
π/2
tan−1(1−e2)
none of these
The correct Answer is:B
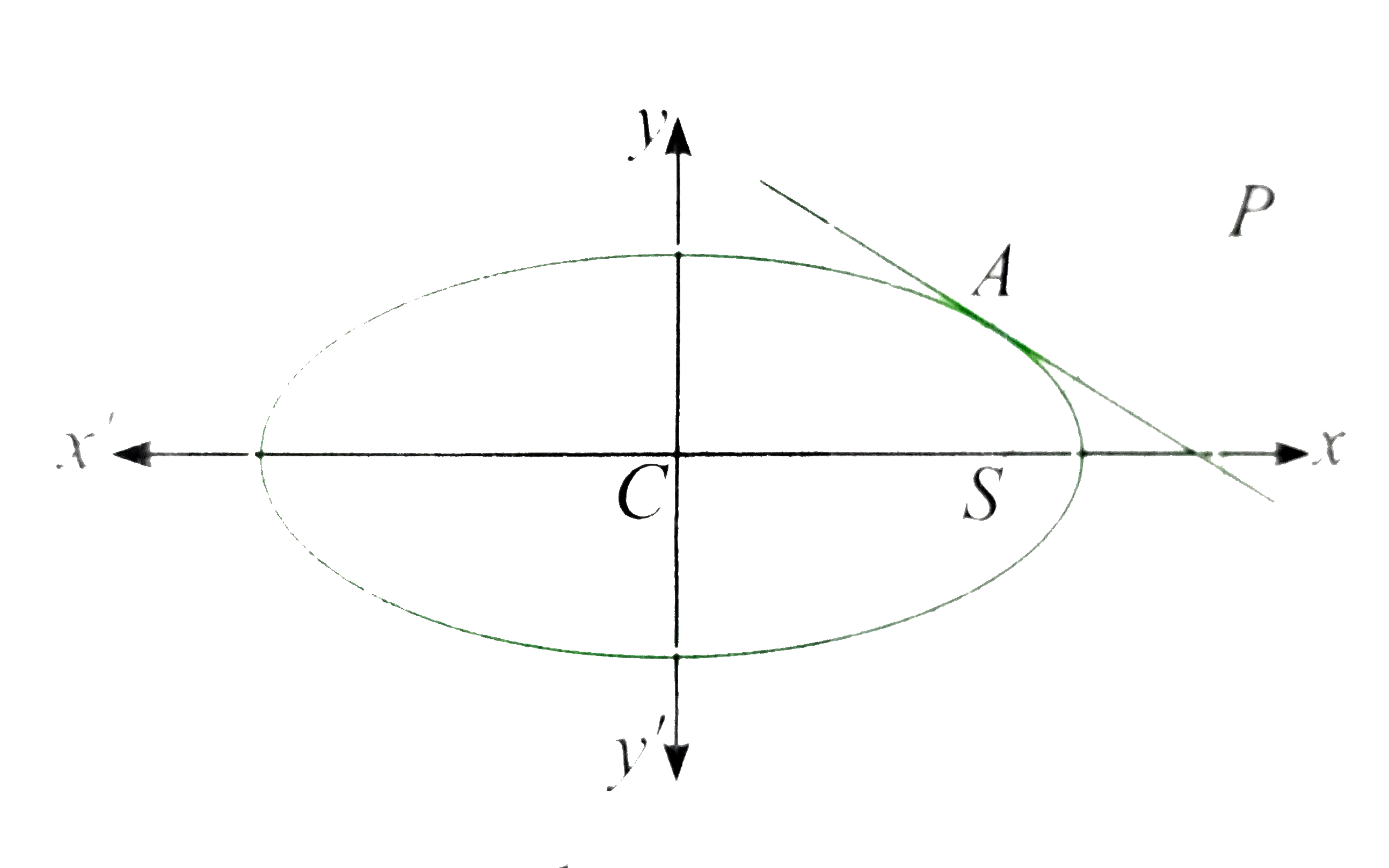
Let the ellipse be
x2a2+y2b2=1
and let A≡(acosθ,bsinθ)
The equation of AC will be
y=batanθx
Solving with x=a/e, we get
P≡(aebetanθ)
Slop of tangent at A=−batanθ
Slope of PS=betanθae−ae=btanθa(1−e2)=abtanθ
So, α=π2
Similar Questions
Let P be any point on a directrix of an ellipse of eccentricity e,S be the corresponding focus, and C the center of the ellipse. The line PC meets the ellipse at A. The angle between PS and tangent a A is α . Then α is equal to tan−1e (b) π2 tan−1(1−e2) (d) none of these
View SolutionLet P be any point on a directrix of an ellipse of eccentricity e, S be the corresponding focus and C be the centre of the ellipse. The line PC meets the ellipse at A. The angle between PS and tangent at A is α. Then α is equal to
View Solution
Knowledge Check
If the lines joining the foci of an ellipse to an end of its minor axis are at right angles , then the eccentricity of the ellipse is e =
A14B1√2C34D2√5Eccentricity of the ellipse whose latus rectum is equal to the distnce between two focus points, is
A√5+12B√5−12C√52D√32IF the distance between a focus and corresponding directrix of an ellipse be 8 and the eccentricity be 12, then length of the minor axis is
A3B4√2C6D16√33
The y-axis is the directrix of the ellipse with eccentricity e=12 and the corresponding focus is at (3,0), equation to its auxilary circle is
View SolutionFind the equation of the ellipse whose eccentricity is 1/2, the focus is (1,1) and the directrix is x−y+3=0.
View SolutionIf P is any point on the ellipse with eccentricity 23 and foci F1,F2 such that PF1+PF2=6 ,then the equation of the ellipse
View SolutionIf α,β are the eccentric angles of the extermities of a focal chord of an ellipse, then eccentricity of the ellipse is
View SolutionThe focus of an ellipse is (-1, -1) and the corresponding directrix is x−y+3=0. If the eccentricity of the ellipse is 1/2, then the coordinates of the centre of the ellipse, are
View Solution
