let P1=⎡⎢⎣100010001⎤⎥⎦,P2=⎡⎢⎣100001010⎤⎥⎦,P3=⎡⎢⎣010100001⎤⎥⎦,P4=⎡⎢⎣010001100⎤⎥⎦,P5=⎡⎢⎣001100010⎤⎥⎦,P6=⎡⎢⎣001010100⎤⎥⎦ and X=6∑k=1Pk⎡⎢⎣213102321⎤⎥⎦PTk Where PTk is transpose of matrix Pk. Then which of the following options is/are correct?
X is a symmetric matrix
if X=⎡⎢⎣111⎤⎥⎦=α⎡⎢⎣111⎤⎥⎦, then α=30
X-30I is an invertible matrix
The sum of diagonal entries of X is 18.
The correct Answer is:A, B, D
Clearly P1=PT1=P−11
P2=PT2=P−12
.
.
.
P6=PT6=P−16
And AT=A where A=⎡⎢⎣213102321⎤⎥⎦
Using formula (A+B)T=AT+BT
XT=(P1APT1+....+P6AP6T)T=P1ATPT1+.....+P6ATPT6=ΞmpliesX is symmetric
Let B=⎡⎢⎣111⎤⎥⎦
XB=P1APT1B+P2APT2B+....+P6APT6B=P1AB+PAB+....+P6AB
XB=(P1+P2+....+P6)⎡⎢⎣636⎤⎥⎦
=⎡⎢⎣6×2+3×2+6×26×2+3×2+6×26×2+3×2+6×2⎤⎥⎦=⎡⎢⎣303030⎤⎥⎦=30B⇒α=30
since X⎡⎢⎣(1),(1),(1)=30⎡⎢⎣111⎤⎥⎦
⇒(X−30I)B=0 has a non trivial solution B=⎡⎢⎣111⎤⎥⎦
⇒|X−30I|=0
X=P1P1APT1+....+P6APT6
trace (x)=tr(P1APT1)+.....+tr(P6APT6)=(2+0+1)+....+(2+0+1)=3×6=18
Related Playlists
Similar Questions
let P1=⎡⎢⎣100010001⎤⎥⎦,P2=⎡⎢⎣100001010⎤⎥⎦,P3=⎡⎢⎣010100001⎤⎥⎦,P4=⎡⎢⎣010001100⎤⎥⎦,P5=⎡⎢⎣001100010⎤⎥⎦,P6=⎡⎢⎣001010100⎤⎥⎦ and X=6∑k=1Pk⎡⎢⎣213102321⎤⎥⎦PTk Where PTk is transpose of matrix Pk. Then which of the following options is/are correct?
View SolutionLet P1=I=⎡⎢⎣100010001⎤⎥⎦,P2=⎡⎢⎣100001010⎤⎥⎦
P3=⎡⎢⎣010100001⎤⎥⎦,P4=⎡⎢⎣010001100⎤⎥⎦
P5=⎡⎢⎣001100010⎤⎥⎦,P6=⎡⎢⎣001010100⎤⎥⎦ and
X=6∑k=1PK⎡⎢⎣213102321⎤⎥⎦PTK
Where , PTK denotes the transpose of the matrix PX. then which of the following option is/are correct ?View SolutionIf P=⎡⎢⎣010021230⎤⎥⎦,Q=⎡⎢⎣123041⎤⎥⎦, find PQ.
View SolutionThe inverse of the matrix ⎡⎢⎣001010100⎤⎥⎦ is (A) ⎡⎢⎣001010100⎤⎥⎦ (B) ⎡⎢⎣00−10−10−100⎤⎥⎦ (C) ⎡⎢⎣100010001⎤⎥⎦ (D) ⎡⎢ ⎢ ⎢⎣120001200012⎤⎥ ⎥ ⎥⎦
View SolutionIf A=⎡⎢⎣010100001⎤⎥⎦, then A−1=
View SolutionIf A=⎡⎢⎣0010−10100⎤⎥⎦ then A−1=
View SolutionIf P=⎡⎢⎣124310001⎤⎥⎦,Q=⎡⎢⎣1−2−3−31900−5⎤⎥⎦then (PQ)−1 equals to
View SolutionA=⎡⎢⎣1000110−24⎤⎥⎦,I=⎡⎢⎣100010001⎤⎥⎦
A−1=16(A2+CA+DI) then C and D equal toView SolutionIf A=⎡⎢⎣001010100⎤⎥⎦ then A6=
View SolutionThe truth table for the following combination of gates is
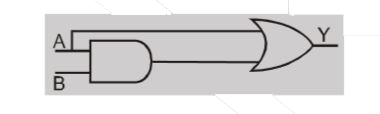
(a) ABY000010101111
(b) ABY000010100111
(c) ABY001011101110
(d) ABY0000111011110View Solution


