Let PQ and QR be diagonals of adjacent faces of a rectangular box, with its centre at O. If $∠ Q O R, ∠ R O P and ∠ P O Q$ are $θ, ϕ and Ψ$ respectively then the value of $' cos θ + cos ϕ + cos Ψ'$ is :

-2

$- \sqrt{3}$

-1

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

Answer

Step by step video, text & image solution for Let PQ and QR be diagonals of adjacent faces of a rectangular box, with its centre at O. If angle QOR, angle ROP and angle POQ are theta, phi and Psi respectively then the value of 'costheta +cos phi+cos Psi' is : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS VECTOR ALGEBRA

Topper's Solved these Questions

Knowledge Check

If $cos θ = \frac{3}{5} and cos ϕ = \frac{4}{5},$ where $θ$ and $ϕ$ are positive acute angles, then $cos \frac{θ - ϕ}{2} =$
A $\frac{7}{\sqrt{2}}$
B $\frac{7}{5 \sqrt{2}}$
C $\frac{7}{\sqrt{5}}$
D $\frac{7}{2 \sqrt{5}}$
In a $Δ P Q R$ , the sides PQ and PR and are produced to S and T respectively. Bisectors of $∠ S Q R and ∠ Q R T$ meet at the point O. If $∠ P = 66^{\circ}$ , then what is the value of $∠ Q O R$ ?
A $47^{\circ}$
B $50^{\circ}$
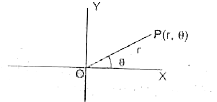
C $57^{\circ}$
D $67^{\circ}$
Let $O P = r and ∠ X O P = θ$ then the position of P in polar coordinate system is represented by $(r, θ)$ OX and O are called the initial line and pole respectively.
If p be the length of perpendicular from origin to line and if $α$ is the angle which the perpendicular to the line makes with the initial line . The equation of line is given by r cos $(θ - α) = p$

Perpendicular distance from pole to the line $\frac{l}{r} = 4 cos θ + 2 sin θ$ is
A $2 \sqrt{5}$
B $\frac{l}{2 \sqrt{5}}$
C $\frac{2 \sqrt{5}}{l}$
Dnone of these

VK JAISWAL-VECTOR & 3DIMENSIONAL GEOMETRY-Exercise-5 : Subjective Type Problems

Home
Ask Doubt
Profile

Let PQ and QR be diagonals of adjacent faces of a rectangular box, with its centre at O. If ∠QOR,∠ROPand∠POQ are θ,ϕandΨ respectively then the value of 'cosθ+cosϕ+cosΨ' is :

The correct Answer is:C

Topper's Solved these Questions

Similar Questions

Knowledge Check

If cosθ=35andcosϕ=45, where θ and ϕ are positive acute angles, then cosθ−ϕ2=

In a ΔPQR, the sides PQ and PR and are produced to S and T respectively. Bisectors of ∠SQRand∠QRT meet at the point O. If ∠P=66∘, then what is the value of ∠QOR?

VK JAISWAL-VECTOR & 3DIMENSIONAL GEOMETRY-Exercise-5 : Subjective Type Problems

Let PQ and QR be diagonals of adjacent faces of a rectangular box, with its centre at O. If $∠ Q O R, ∠ R O P and ∠ P O Q$ are $θ, ϕ and Ψ$ respectively then the value of $' cos θ + cos ϕ + cos Ψ'$ is :

If $cos θ = \frac{3}{5} and cos ϕ = \frac{4}{5},$ where $θ$ and $ϕ$ are positive acute angles, then $cos \frac{θ - ϕ}{2} =$

In a $Δ P Q R$ , the sides PQ and PR and are produced to S and T respectively. Bisectors of $∠ S Q R and ∠ Q R T$ meet at the point O. If $∠ P = 66^{\circ}$ , then what is the value of $∠ Q O R$ ?