Let S be the set of positive rational numbers and is defined by a∗b=ab2. Then find the identity element and the inverse of 2. Solution in Tamil
Step by step video & image solution for Let S be the set of positive rational numbers and is defined by a ** b=(ab)/2. Then find the identity element and the inverse of 2. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - SURA PUBLICATIONCHAPTER - DISCRETE MATHEMATICS EXERCISE - 3 MARKS5videos
DISCRETE MATHEMATICS
- BOOK - SURA PUBLICATIONCHAPTER - DISCRETE MATHEMATICS EXERCISE - 5 MARKS2videos
DISCRETE MATHEMATICS
- BOOK - SURA PUBLICATIONCHAPTER - DISCRETE MATHEMATICS EXERCISE - MATCH THE FOLLOWING4videos
DISCRETE MATHEMATICS
- BOOK - SURA PUBLICATIONCHAPTER - DIFFERENTIALS AND PARTIAL DERIVATIVES EXERCISE - 5 MARKS4videos
DIFFERENTIALS AND PARTIAL DERIVATIVES
- BOOK - SURA PUBLICATIONCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - ADDITIONAL QUESTIONS ( 5 MARKS)6videos
INVERSE TRIGONOMETRIC FUNCTIONS
Similar Questions
Write the truth value for each of the following statements.
(1) 3+5=8 and √2 is an irrational number.
(2) 5 is a positive integer or a square is a rectangle.
(3) Chennai is not a Tamilnadu.01:42View SolutionLet S be a non-empty set and 0 be a binary operation on s defined by x 0 y =x, x, y∈S. Determine whether 0 is commutative and association.
01:30View Solution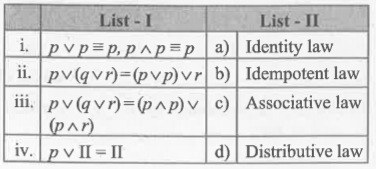
The correct match is01:08View SolutionIf u=tan−1(x3+y3x−y), Prove that x∂u∂x+y∂u∂y=sin2u.
01:56View SolutionFind the domain of the following functions
f(x)=sin−1(2x−3)02:38View SolutionLet '⋅' be a binary operation on Q0 (set of all non-zero rational numbers) defined by a⋅b=ab4 for all a,b∈Q0. Then, find the identity element in Q0 inverse of an element in Q0.
03:36View SolutionLet S be the set of all rational numbers except 1 and * be defined on S by a⋅b=a+b−ab, for alla,b∈S. Find its identity element
01:18View SolutionFind the identity element in set Q+ of all positive rational numbers for the operation * defined by a⋅b=ab2 for all a,b∈Q+.
01:11View SolutionFind the identity element in the set of all rational numbers except -1 with respect to * defined by a⋅b=a+b+ab .
03:18View Solutionयदि द्विआधारी ∗ धनात्मक वास्तविक संख्याओं के समुच्चय R+ के इस प्रकार परिभाषित है की a∗b=ab5∀a,b∈R+.R+ में तत्समक अवयव और प्रतिलोम अवयव ज्ञात कीजिए।
03:29View Solutionपरिमेय संख्याओं के समुच्चय Q में संक्रिया 'o' इस प्रकार परिभाषित है-
aob=a+b−ab,∀a,b∈Q. इसका तत्समक तथा प्रतिलोम अवयव ज्ञात कीजिए |02:23View SolutionLet * be a binary operation defined on the set of non-zero rational number, by a∗b=ab4. Find the identity element.
01:32View Solutionधनात्मक परिमेय संख्याओं के समुच्चय Q+ में संक्रिया * के लिए जो a * b =ab2,∀a,b∈Q+ से परिभाषित है, तत्समक अवयव ज्ञात कीजिए।
01:38View Solutionपरिमेय संख्याओं के समुच्चय Q में संक्रिया o इस प्रकार परिभाषित है -
aob=a+b−ab,∀a,b∈Q ,
इसका तत्समक तथा प्रतिलोम अवयव ज्ञात कीजिए।05:55View SolutionLet '⋅' be a binary operation on Q0 (set of all non-zero rational numbers) defined by a⋅b=ab4 for all a,b∈Q0. Then, find the identity element in Q0 inverse of an element in Q0.
04:13View Solution

