Let S= set of point inside the sqare, T= set of points inside the triangles and C= the set of point inside the circle, if the triangle and circle intersect each other are contained in the square, then (a) S∩T∩C=ϕ(b)S∪T∪C=C(c) S∪T∪C=S(d)S∪T=S∩C
Step by step video & image solution for Let S= set of point inside the sqare, T= set of points inside the triangles and C= the set of point inside the circle, if the triangle and circle intersect each other are contained in the square, then (a) S nn T nn C = phi(b)S uu T uu C = C(c) S uu T uu C = S(d) S uu T = S nn C by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
Let S=Set of points inside the square, T=set of points inside the triangle and C=the set of points inside the circle. If the triangle and circle intersect each other and are contained in a square. Then (i) S∩T∩C=ϕ (ii) S∪T∪C=C (iii) S∪T∪C=S (iv) S∪T=S∩C
AS∩T∩C=ϕBS∪T∪C=CCS∪T∪C=SDS∪T=S∩C
For all sets A,B and C, if A⊂B, then A∪C⊂B∪C.
View SolutionLet C be incircle of ABC. If the tangents of lengths t1,t2andt3 are drawn inside the given triangle parallel to sidese a,bandc , respectively, the t1a+t2b+t3c is equal to 0 (b) 1 (c) 2 (d) 3
View SolutionTangents and normal drawn to the parabola y2=4ax at point P(at2,2at),t≠0, meet the x-axis at point TandN, respectively. If S is the focus of theparabola, then (a) SP=ST≠SN (b) SP≠ST=SN (c) SP=ST=SN (d) SP≠ST≠SN
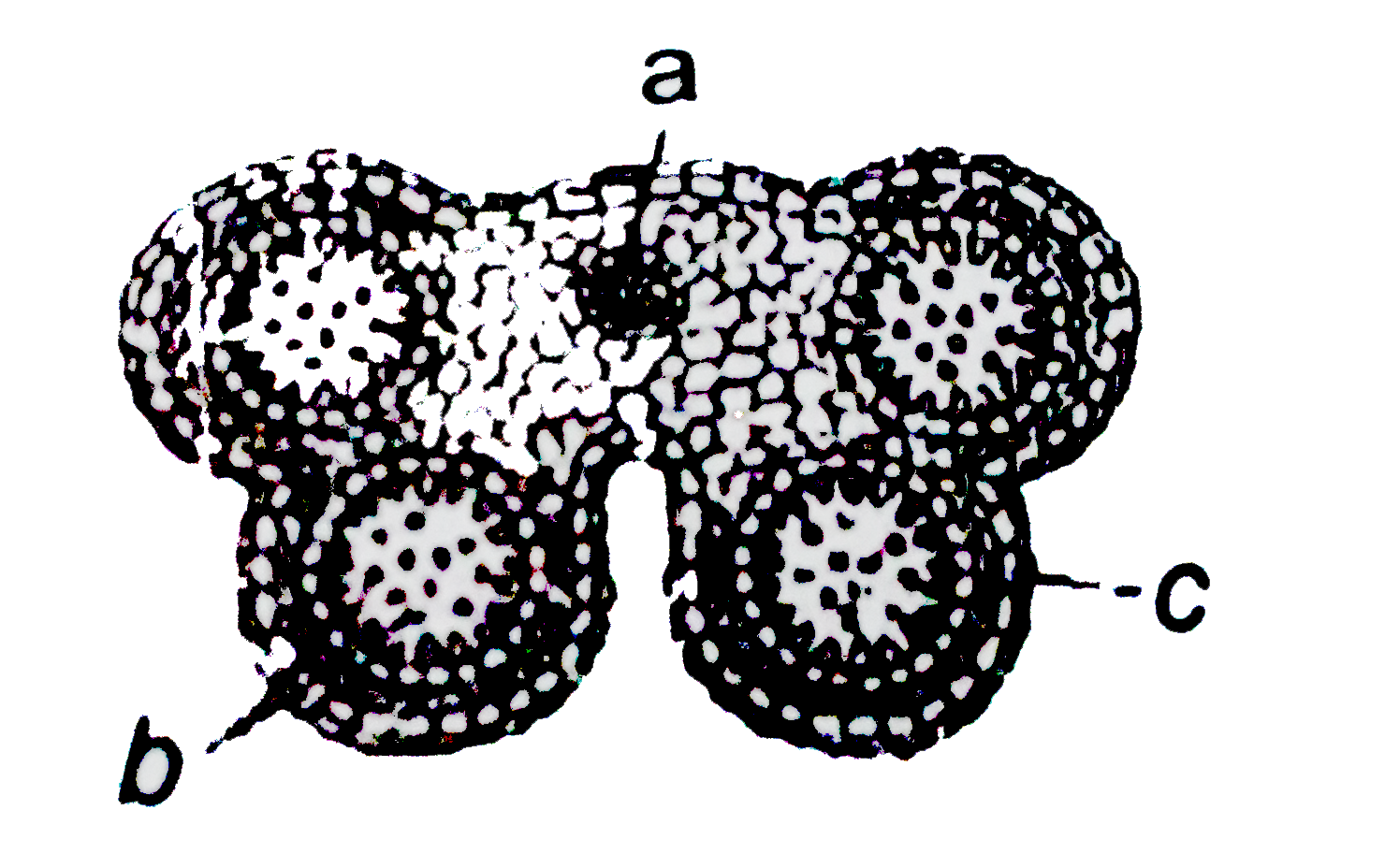
View SolutionIn T.S anther, identify a, b and c
View SolutionLet A,B and C be sets such that ϕ≠A∩B⊆C. Then which of the following statements is not true?
View SolutionLet A =(a,b,c),B=(b,d,e)andC=(e,f,g) , verify that :
(A∪B)∪C=A∪(B∪C)
View SolutionLet U= {a,b,c,d,e,f,g} be the universal set and let its subsets be A = {a,b,d,e} and B = {b,e,g}
Verify that : (A∩B)'=(A'∪B')
View Solution