Let S1 and S2 be the two switches and let their probabilities of working be given by P(S_(1))=⅘ and P(S2)=.9/10. Find the probability that the current flows from the terminal a to terminal A to terminal B when S1 and S2 are installed in series, shown as follows :
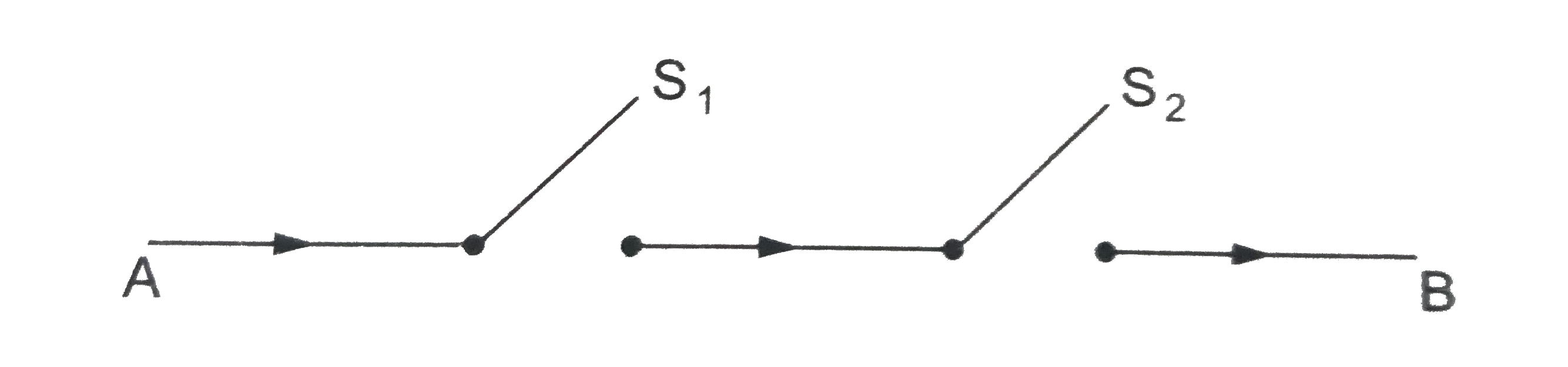
The correct Answer is:1825
P( current flows from A to B)
=P(S1 is closed and S2 is closed)
=P(S1andS2)=P(S1)×PS2.
Topper's Solved these Questions
- PROBABILITYBook:RS AGGARWALChapter:PROBABILITYExercise:Exercise 29B
Explore 23 Videos
- METHODS OF INTEGRATION Book:RS AGGARWALChapter:METHODS OF INTEGRATION Exercise:Objective Questions Ii
Explore 56 Videos
- PROBABILITY DISTRIBUTIONBook:RS AGGARWALChapter:PROBABILITY DISTRIBUTIONExercise:Exercise 32
Explore 32 Videos
Similar Questions
Knowledge Check
Let S1 and S2 be the two slits in Young's double-slit experiment. If central maxima is observed at P and angle ∠S1PS2=θ, then fringe width for the light of wavelength λ will be
Aλ/θBλθC2λ/θDλ/2θLet S1 and S2 be the two slits in Young's double-slit experiment. If central maxima is observed at P and angle ∠S1PS2=θ, then fringe width for the light of wavelength λ will be (assume θ to be a small angle)
Aλ/θBλθC2λ/θDλ/2θLet S1 and S2 be the foci of a rectangular hyperbola, which has the centre at Q , then for and point P on the hyperbola S1P equals to
AS1S22BQS21CQP2D4QP2
Let S1=0andS2=0 be two circles intersecting at P(6,4) and both are tangent to x-axis and line y=mx(where m>0). If product of radii of the circles S1=0andS2=0 is 523 then find the value of m.
View SolutionOnly three students, S1,S2andS3 appear at a compettive examination. The probability of S1 coming first is 3 times that of S2 and the probability of S2 coming first is three times that of S3. Find the probability of each coming first. Also find the probability that S1orS2 comes first.
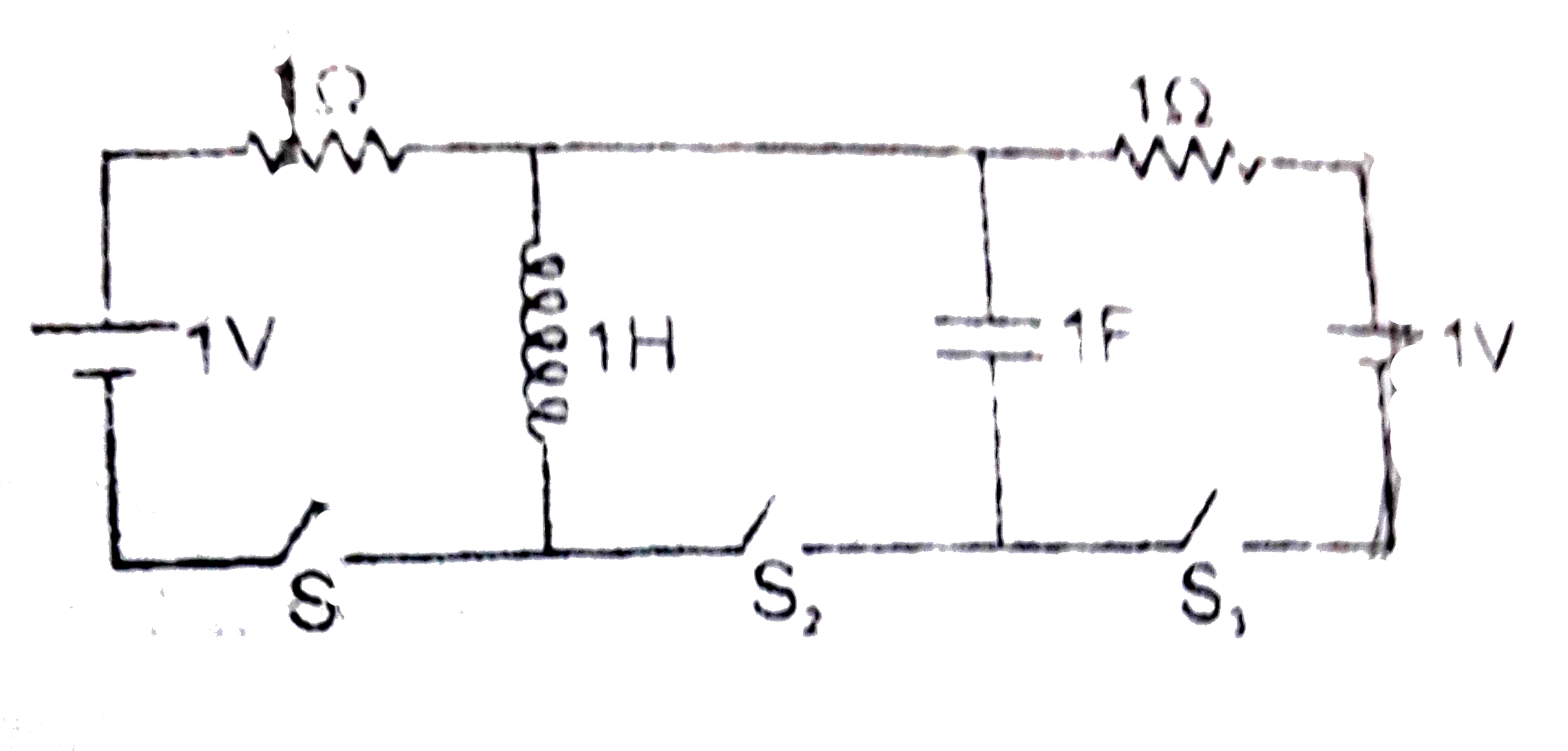
View SolutionIn the circuit shown switches S1 and S2 have been closed for 1sec and S2 remained open.Just after 1 second is over switch S2 is closed and S1,S3 are opened.Find after that instant The charge on the upper plate of the capacitor as function of time taking the instant of switching on of S2 and switching off all time switches to be t=0 is q=x×10−2cos(t+π4).Findout value of x.
View SolutionGourang made an electric circuit with three bulbs B1,B2 and B3 a cell and two switches S1 and S2 as shown in figure. He notes his observation when

(a) S1 is closed and S2 is open,
(b) S2 is closed and S1 is open.
He also found that a bulb whose failure made the circuit 'open' irrespective of the status of S1 and S2 . What are his observation.
View SolutionIf S1,S2,S3 be respectively the sums of n, 2n and 3n terms of a G.P., prove that S1(S3−S2)=(S2−S1)2.
View Solution
