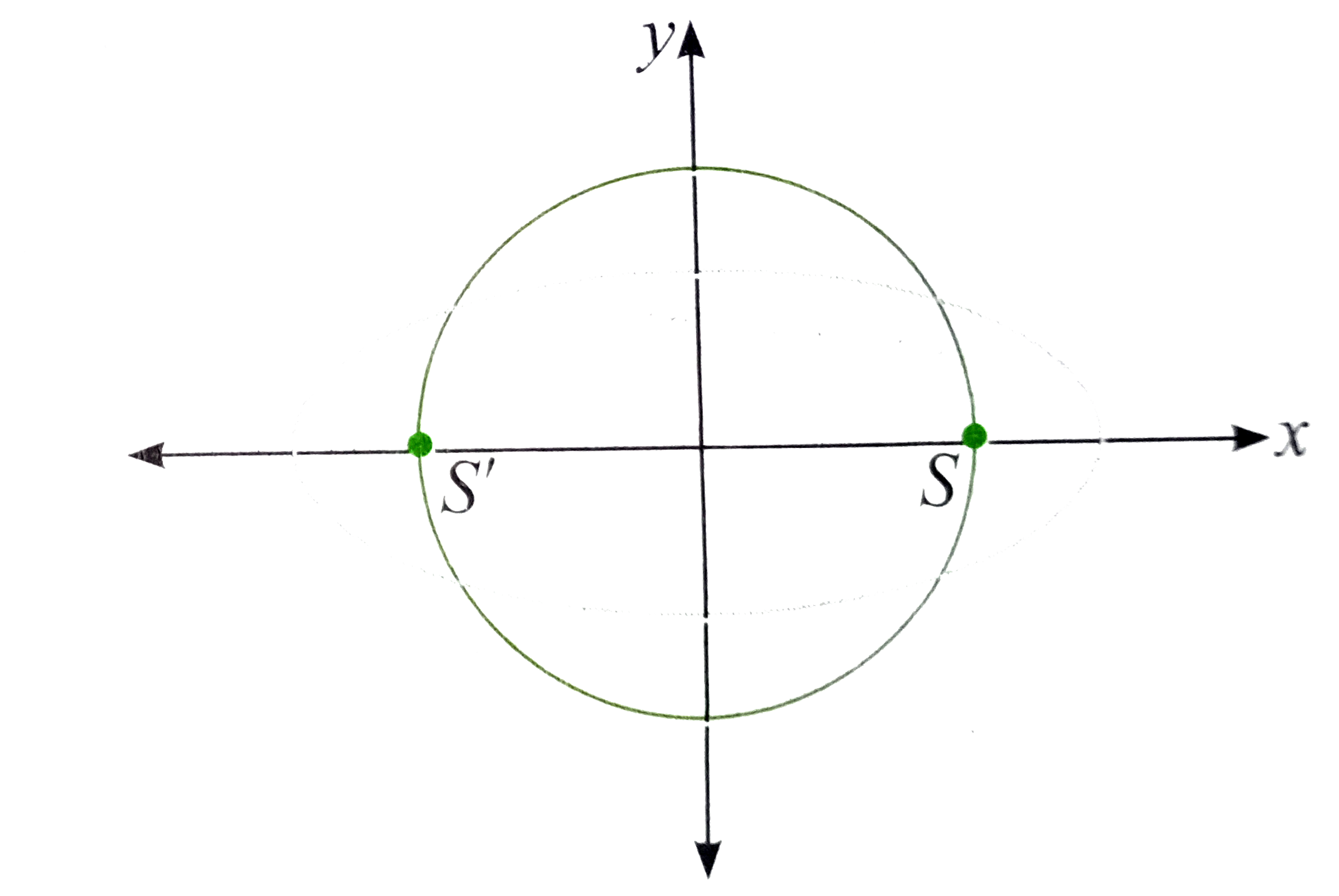
Let SandS'
be two foci of the ellipse x2a3+y2b2=1
. If a circle described on SS′
as diameter intersects the ellipse at real and distinct points, then
the eccentricitye
of the ellipse satisfies
e=1/√2
e∈(1√2,1)
e∈(0,1/√2)
none of these
The correct Answer is:B
The radius of the circle having SS' as diameter is r=ae.
If it cust an ellipse, then
r>b
or ae>b
ore2>b2a2
or e2>1−e2
ore2>12
or e=t1√2
or∈(1√2,1)
Similar Questions
Let SandS' be two foci of the ellipse x2a3+y2b2=1 . If a circle described on SS′ as diameter intersects the ellipse at real and distinct points, then the eccentricitye of the ellipse satisfies c=1√2 (b) e∈(1√2,1) e∈(0,1√2) (d) none of these
View SolutionEllipse x2a2+y2b2=1(a>b) Equation of the circle described on major axis as diameter is
View Solution
Knowledge Check
Let S and S'' be the fociof the ellipse x2a2+y2b2=1 whose eccentricity is e. P is a variable point on the ellipse. Consider the locus the incenter of ΔPSS'' The eccentricity of the locus of the P is
A√2e1−eB√2e1+eC1Dnone of theseA circle is drawn with the two foci of an ellipse x2a2+y2b2=1 at the end of diameter. What is the equation of the circle?
Ax2+y2−a2+b2Bx2+y2=a2−b2Cx2+y2=2(a2+b2)Dx2+y2=2(a2−b2)If the ellipse of the auxiliary circle of the ellipse x2a2+y2b2=1(a>b) is twice the area of the ellipse, then the eccentricity of the ellipse is
A1√2B√32C1√3D12
If S and S' are two foci of the ellipse x2a2+y2b2=1 and B is and end of the minor axis such that DeltaBSS' is equilateral, then write the eccentricity of the ellipse.
View SolutionThe line 3x−4y=12 is a tangent to the ellipse with foci (-2, 3) and (-1, 0). Find the eccentricity of the ellipse.
View SolutionIf the foci of an ellipse x29+y216=1 are ends of diameter of a circle then finds the radius of the circle
View SolutionS and T are the foci of the ellipse (x2a2)+(y2b2)=1 and B is an end of the minor axis. If STB is equilateral triangle, then eccentricity of the ellipse is
View Solutionif S and S are two foci of an ellipse x2a2+y2b2=1 ( altb) and P(x1,y1) a point on it then SP+ S'P is equal to
View Solution
