Let denote the sum of the infinite geometric series whose first term is and the common
ration is then the value of |(k^2-3k+1)S_k| is ____________Solution in Bengali
The correct Answer is:3
Topper's Solved these Questions
- PROGRESSION AND SERIESBOOK - CENGAGE PUBLICATIONCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Videos
- PROBABILITY IIBOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY IIEXERCISE - MULTIPLE CORRECT ANSWER TYPE
6 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE PUBLICATIONCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (Numerical Value Type)
3 Videos
Similar Questions
Match the statements /expression given in List I with the values given in List II.

View SolutionLet EandF be two independent events. The probability that exactly one of them occurs is 1125 and the probability if none of them occurring is 225. If P(T) denotes the probability of occurrence of the event T, then (a) P(E)=45,P(F)=35 (b) P(E)=15,P(F)=25 (c) P(E)=25,P(F)=15 (d) P(E)=35,P(F)=45
View SolutionLet ABCandABC' be two non-congruent triangles with sides AB=4,AC=AC′=2√2 and angle B=300 . The absolute value of the difference between the areas of these triangles is
View SolutionFind the sum of first 100 terms of the series whose general term is given by ak=(k2+1)k!
View SolutionLet Sk, where k=1,2,....,100, denotes the sum of the infinite geometric series whose first term is k−1k! and the common ratio is 1k. Then, the value of 1002100!+100∑k=2∣∣(k2−3k+1)Sk∣∣ is....
View SolutionLet Sk be sum of an indinite G.P whose first term is 'K' and commmon ratio is 1k+1. Then Σ10k=1Sk is equal to _________.
View Solutionमान लीजिये कि Sk,k=1,2,...,100 उस अनन्त गुणोत्तर श्रेणी का योग प्रदर्शित करता है जिसका प्रथम पद k−1k!तथा सार्वअनुपात 1kहै, तो 1002100!+Σ100k=1∣∣(k2−3k+1)Sk∣∣का मान क्या है ?
View Solutionमाना की Sk=1,2,……..100 उस अनंत गुणोत्तर श्रेणी का योग प्रदर्शित करता है जिसका प्रथम पद k−1k! तथा सार्व अनुपात 1k है तो 1002100!+100∑k=1∣∣(k2−3k+1)Sk∣∣का मान है
View Solutionयदि एक अनंत गुणोत्तर श्रेणी जिसका प्रथम पद k और सरवणुपात kk+1(k>0) का योग प्रदर्शित करता है तब ∞∑k=1(−1)kSkका मान होगा
View Solutionमाना की Sk=1,2,……..100 उस अनंत गुणोत्तर श्रेणी का योग प्रदर्शित करता है जिसका प्रथम पद k−1k! तथा सार्व अनुपात 1k है तो 1002100!+100∑k=1∣∣(k2−3k+1)Sk∣∣का मान है
View SolutionFind the sum of first 100 terms of the series whose general term is given by ak=(k2+1)k!
View SolutionLet Sk, where k=1,2,....,100, denotes the sum of the infinite geometric series whose first term is k−1k! and the common ratio is 1k. Then, the value of 1002100!+100∑k=2∣∣(k2−3k+1)Sk∣∣ is....
View SolutionLet Sk be sum of an indinite G.P whose first term is 'K' and commmon ratio is 1k+1. Then Σ10k=1Sk is equal to _________.
View SolutionLet Sk,k=1,2,….100 denote the sum of the infinite geometric series whose first term is k−1K! and the common
ration is 1k then the value of (100)2100!+Σ100k=1∣∣(k2−3k+1)Sk∣∣ is ____________
View SolutionLet sk,k=1,2,3,…,100 denote the sum of the infinite geometric series whose first term is k−1⌊k and the common ratio is 1k. Then, the value of
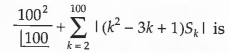 is
is
View SolutionLet Sk be the sum of an infinite G.P. series whose first term is k and common ratio is kk+1(k>0). Then the value of ∞∑k=1(−1)ksk is equal to
View Solution
