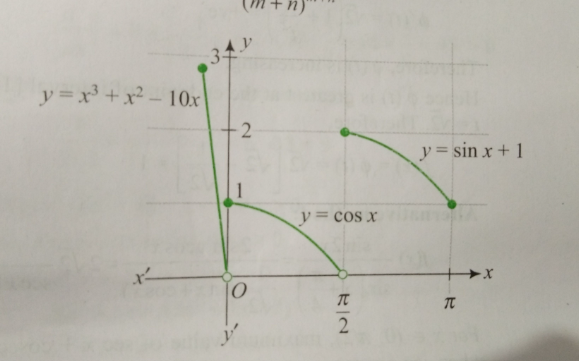
Let the function f(x) be defined as follows:f(x)= x^3 +x^2 −10x,−1≤x<0 cosx,0≤x< 2 π 1+sinx 2 π ≤x≤π , then which of the following statement(s) is/are correct
a local minimum at x=π/2
a global maximum at x=π/2
a absolute maximum at x=-1
a absolute maximum at x=π
The correct Answer is:3
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Multiple correct answers type48videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Numerical Value Type24videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Concept Application Exercise 6.75videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - Single Correct Answer Type46videos
METHODS OF DIFFERENTIATION
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type6videos
MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONS
Similar Questions
Let function f(x) be defined as
f(x)=∣∣sin−1x∣∣+cos−1(1x). Then which of the following is /are TRUE.View SolutionA function is defined as follows
f(x)={x3x2<1xx2≥1 then function isView SolutionLet f(x) be defined as follows f(x)={x6x2>1x3x2≤1 Then f(x) is
View SolutionA function f(x) is defined as f(x)=x2+3. Find f(0),F(1),f(x2),f(x+1) and f(f(1)).
View SolutionLet f:R→R be a function defined by f(x)=x3+x2+3x+sinx. Then f is
View SolutionLet f:R→R be a function defined by f(x)=x3+x2+3x+sinx. Then f is
View SolutionLet a function f:R→R be defined as f(x)=x+sinx. The value of ∫2π0f−1(x)dx will be:
View SolutionThe function f:R→R defined as f(x)=x2−x+1x2+x+1 is
View SolutionThe function f:R→R defined by f(x)=(x−1)(x−2)(x−3) is
View SolutionLet f1:R→R,f2:[0,∞)→R,f3:R→R be three function defined as
f1(x)={|x|x<0exx≥0,f2(x)=x2,f3(x)={f2(f1(x))x<0f2(f1(x))−1x≥0 then f3(x) is:View Solution