Let $V_{1}$ be the volume of a given right circular cone with O as the centre of the base and A as its apex. Let $V_{2}$ be the maximum volume of the right circular cone inscribed in the given cone whose apex is O and whose base is parallel to the base of the given cone. then the ratio $V_{2} / V_{1}$ is -

A

$\frac{3}{25}$

B

$\frac{4}{9}$

C

$\frac{4}{27}$

D

$\frac{8}{27}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

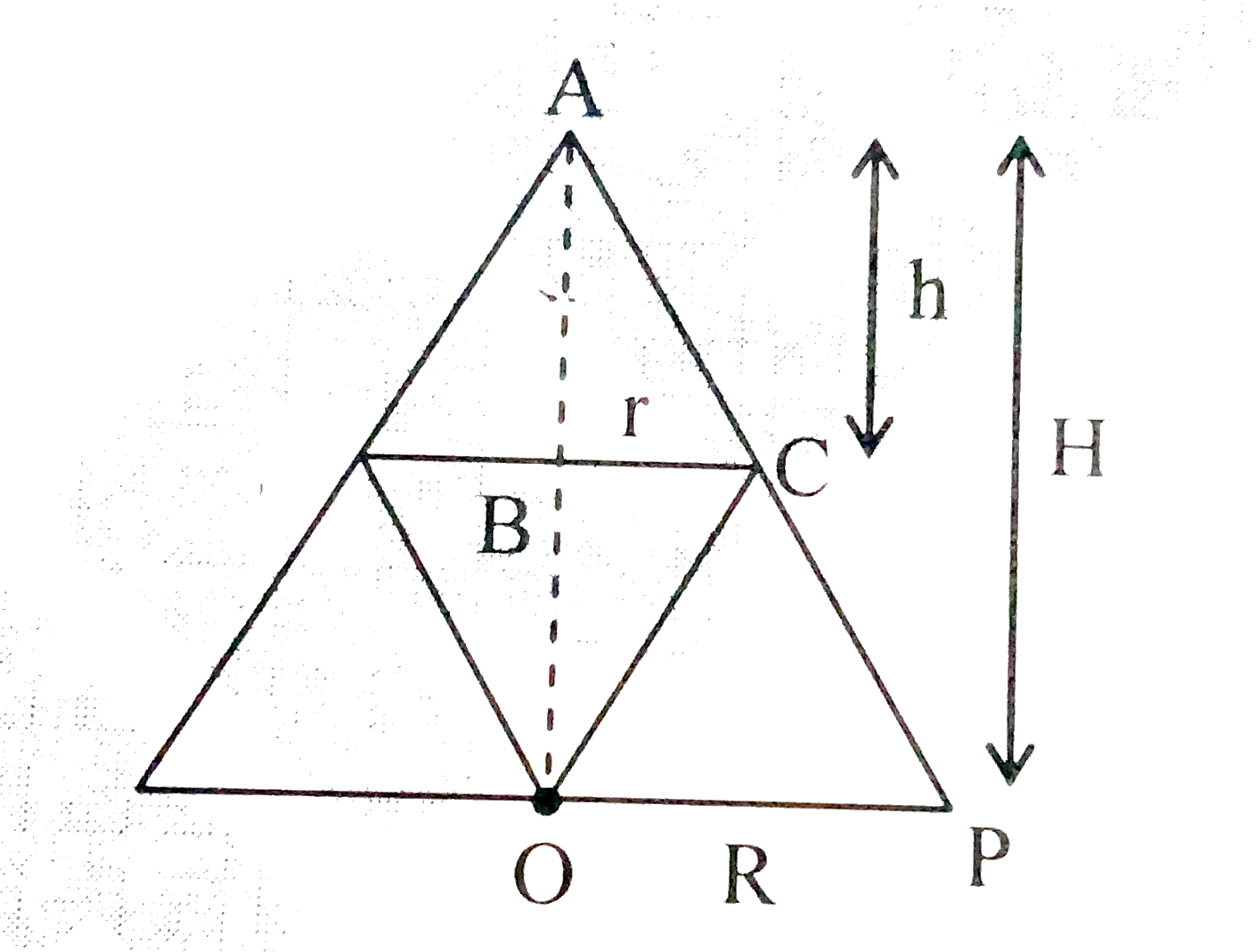
$Δ A B C$ and $Δ A O P$ are similar
$\frac{h}{r} = \frac{H}{R} \Rightarrow h = \frac{r H}{R}$
$V_{2} = \frac{1}{3} π r^{2} (H - h) = \frac{π}{3} r^{2} H (1 - \frac{r}{R}) = \frac{π H}{3} (r^{3} - \frac{r^{3}}{R})$
$\frac{d V^{2}}{d r} = 2 r - \frac{3 r^{2}}{R} = 0, r = \frac{2 R}{3}$
$V_{2 max} = \frac{4 π R^{2} H}{81}$
$V_{1} = \frac{π R^{2} H}{3}$
$∴ \frac{V_{2}}{V_{1}} = \frac{4}{27}$

Updated on:21/07/2023

|

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

KVPY PREVIOUS YEAR-KVPY-exercise

Home
Ask Doubt
Profile