Let →u=u1ˆi+u2ˆj+u3ˆk be a unit vector in R3and→w=1√6(ˆi+ˆj+2ˆk) , Given that there exists a vector →v in R3 such that |→u×→v|=1and→w.(→u×→v)=1 which of the following statements is correct ?
There is exactly one choice for such →v
There are exactly two for such →v
There are exactly four such →v
There are infinitely many choices for such →v
The correct Answer is:D
To solve the problem step by step, we will analyze the given conditions and derive the necessary conclusions.
Step 1: Understand the given vectors
We are given:
- →u=u1^i+u2^j+u3^k is a unit vector in R3.
- →w=1√6(^i+^j+2^k).
Since →u is a unit vector, we have:
|→u|=√u21+u22+u23=1.
Step 2: Analyze the conditions
We are given two conditions:
1. |→u×→v|=1
2. →w⋅(→u×→v)=1
Step 3: Use the first condition
From the first condition |→u×→v|=1, we know that the magnitude of the cross product of →u and →v is equal to 1. The magnitude of the cross product can be expressed as:
|→u×→v|=|→u||→v|sinθ,
where θ is the angle between →u and →v. Since |→u|=1, we have:
|→v|sinθ=1.
Step 4: Use the second condition
From the second condition →w⋅(→u×→v)=1, we can substitute →w and analyze the dot product:
1√6(^i+^j+2^k)⋅(→u×→v)=1.
This implies:
^i+^j+2^k⋅(→u×→v)=√6.
Step 5: Relate the two conditions
From the first condition, we have |→v|sinθ=1. This means that |→v| must be at least 1sinθ.
Step 6: Conclusion
Since both conditions must hold, we conclude that there are infinitely many vectors →v that satisfy these conditions, as the angle θ can vary while still satisfying |→u×→v|=1 and →w⋅(→u×→v)=1.
Final Answer
The correct statement is that there are infinitely many vectors →v that satisfy the given conditions.
We are given:
- →u=u1^i+u2^j+u3^k is a unit vector in R3.
- →w=1√6(^i+^j+2^k).
|→u|=√u21+u22+u23=1.
We are given two conditions:
1. |→u×→v|=1
2. →w⋅(→u×→v)=1
From the first condition |→u×→v|=1, we know that the magnitude of the cross product of →u and →v is equal to 1. The magnitude of the cross product can be expressed as:
|→u×→v|=|→u||→v|sinθ,
where θ is the angle between →u and →v. Since |→u|=1, we have:
|→v|sinθ=1.
From the second condition →w⋅(→u×→v)=1, we can substitute →w and analyze the dot product:
1√6(^i+^j+2^k)⋅(→u×→v)=1.
This implies:
^i+^j+2^k⋅(→u×→v)=√6.
From the first condition, we have |→v|sinθ=1. This means that |→v| must be at least 1sinθ.
Since both conditions must hold, we conclude that there are infinitely many vectors →v that satisfy these conditions, as the angle θ can vary while still satisfying |→u×→v|=1 and →w⋅(→u×→v)=1.
The correct statement is that there are infinitely many vectors →v that satisfy the given conditions.
Topper's Solved these Questions
- SCALER AND VECTOR PRODUCTS OF TWO VECTORS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SCALER AND VECTOR PRODUCTS OF TWO VECTORS EXERCISE - Section I - Solved Mcqs
12 Videos
- SCALAR AND VECTOR PRODUCTS OF THREE VECTORS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SCALAR AND VECTOR PRODUCTS OF THREE VECTORS EXERCISE - Exercise
63 Videos
- SOLUTIONS OF TRIANGLES BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SOLUTIONS OF TRIANGLES EXERCISE - Exercise
20 Videos
Similar Questions
Let →u=u1ˆi+u2ˆj be a unit vector in xy plane and →w=1√6(ˆi+ˆj+2ˆk) . Given that there exists a vector →v " in " R3 " such that |→u×→v|=1 and →w. (→u×→v)=1 , then
View SolutionLet →u=u1ˆi+u3ˆk be a unit vector in xz-plane and →q=1√6(ˆi+ˆj+2ˆk). If there exists a vector →c in such that |→u×→c|=1and→q.(→u×→c)=1 .Then
View SolutionLet →uand→v be unit vectors such that →u×→v+→u=→wand→w×→u=→v . Find the value of [→u→v→w]
View SolutionIf →u=2ˆi−2ˆj+3ˆk and the final velocity is →v=2ˆi−4ˆj+5ˆk and it is covered in a time of 10 sec, find the acceleration vector.
View SolutionFigure shows the orientation of two vectors u and v in the XY plane.
if →u=aˆi+bˆj and →v=pˆi+qˆj
which of the following is correct?
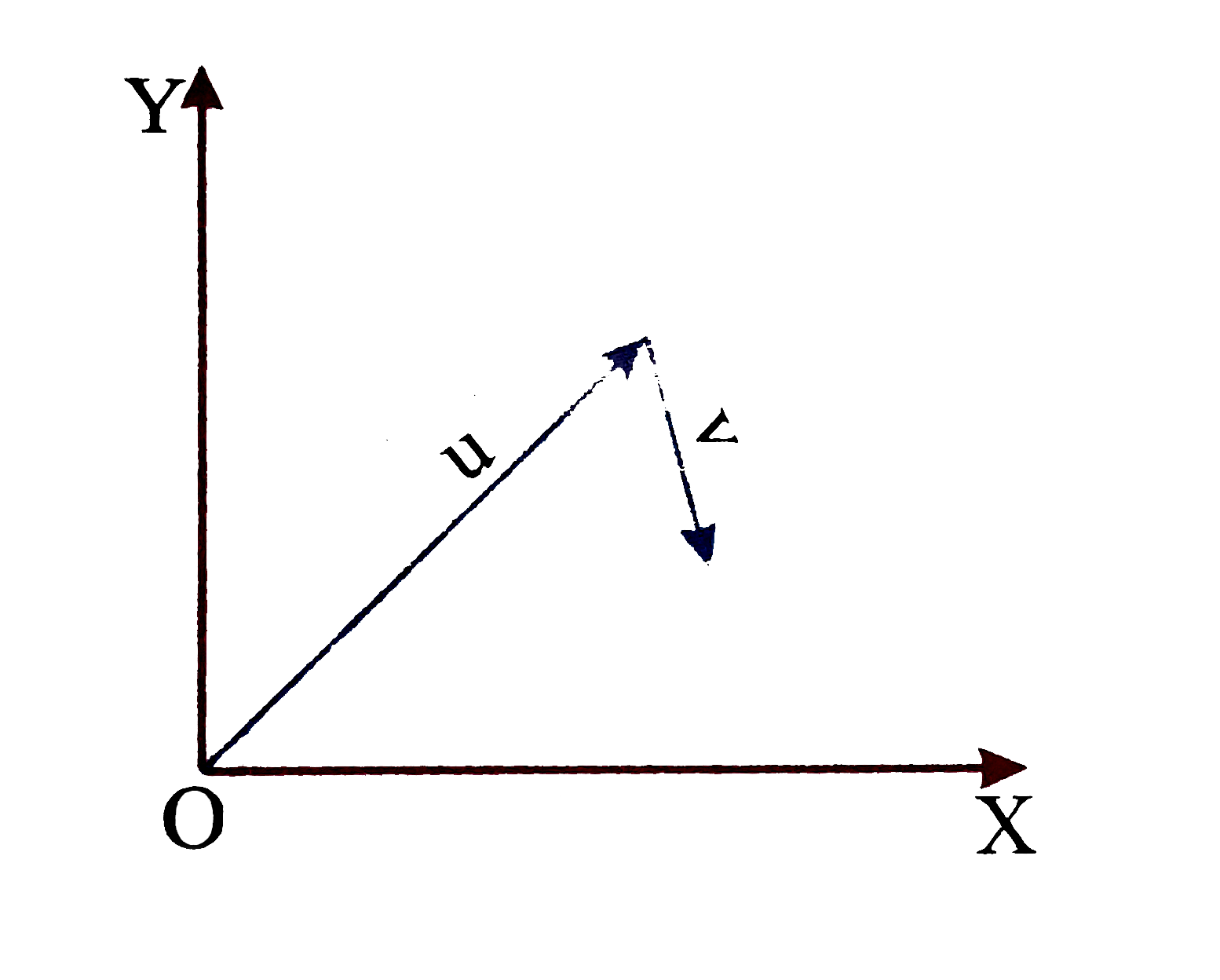
View SolutionFigure shows the orientation of two vectors u and v in the XY plane.
if →u=aˆi+bˆj and →v=pˆi+qˆj
which of the following is correct?

View SolutionLet →u=ˆi+ˆj,→v=ˆi−ˆjand→w=ˆi+2ˆj+3ˆk If ˆn isa unit vector such that →u.ˆn=0and→v.ˆn=0, then |→w.ˆn| is equal to
View SolutionFor three vectors, →u,→vand→w which of the following expressions is not equal to any of the remaining three ?
View SolutionIf →a=2ˆi−3ˆj−1ˆkand→b=ˆi+4ˆj−2ˆk then →a×→b is
View SolutionLet →u=ˆi+ˆj,→v=ˆi−ˆjaandˆi−ˆjand→w=ˆi+2ˆj+3ˆk If ˆn isa unit vector such that →u.ˆn=0and→n.ˆn=0, then |→w.ˆn| is equal to
View Solution
