Let x=33n . The index n is given a positive integral value at random. The probability that the value of x will have 3 in the units place is
12
13
14
none of these
The correct Answer is:C
To solve the problem, we need to determine the probability that the value of x=33n has 3 in the units place when n is a positive integer.
1. Identify the Units Digit of Powers of 33:
We first need to find the units digit of 33n for different values of n. The units digit of a number is determined by the units digit of its base raised to the power.
- For n=1:
331=33(units digit is 3)
- For n=2:
332=1089(units digit is 9)
- For n=3:
333=35937(units digit is 7)
- For n=4:
334=1185921(units digit is 1)
2. Observe the Pattern:
We can observe that the units digits repeat every 4 powers:
- n=1: 3
- n=2: 9
- n=3: 7
- n=4: 1
Thus, the sequence of units digits for 33n is: 3, 9, 7, 1.
3. Determine the Cycle:
The pattern of units digits (3, 9, 7, 1) repeats every 4 values of n. Therefore, we can conclude that:
- For n≡1mod4, the units digit is 3.
- For n≡2mod4, the units digit is 9.
- For n≡3mod4, the units digit is 7.
- For n≡0mod4, the units digit is 1.
4. Calculate the Probability:
Out of the 4 possible outcomes (3, 9, 7, 1), only one outcome (3) corresponds to having 3 in the units place. Therefore, the probability P that the units digit of 33n is 3 is given by:
P(units digit is 3)=Number of favorable outcomesTotal outcomes=14
Final Answer:
The probability that the value of x=33n will have 3 in the units place is 14.
---
We first need to find the units digit of 33n for different values of n. The units digit of a number is determined by the units digit of its base raised to the power.
331=33(units digit is 3)
- For n=2:
332=1089(units digit is 9)
- For n=3:
333=35937(units digit is 7)
- For n=4:
334=1185921(units digit is 1)
We can observe that the units digits repeat every 4 powers:
- n=1: 3
- n=2: 9
- n=3: 7
- n=4: 1
The pattern of units digits (3, 9, 7, 1) repeats every 4 values of n. Therefore, we can conclude that:
- For n≡1mod4, the units digit is 3.
- For n≡2mod4, the units digit is 9.
- For n≡3mod4, the units digit is 7.
- For n≡0mod4, the units digit is 1.
Out of the 4 possible outcomes (3, 9, 7, 1), only one outcome (3) corresponds to having 3 in the units place. Therefore, the probability P that the units digit of 33n is 3 is given by:
P(units digit is 3)=Number of favorable outcomesTotal outcomes=14
The probability that the value of x=33n will have 3 in the units place is 14.
Topper's Solved these Questions
- PROBABILITY BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROBABILITY EXERCISE - Section- II (Assertion -Reason Types MCQs)
15 Videos
- PROBABILITY BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROBABILITY EXERCISE - Section I - Mcqs
89 Videos
- PROBABILITY BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROBABILITY EXERCISE - Chapter Test
45 Videos
- PERMUTATIONS AND COMBINATIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Chapter Test
60 Videos
- QUADRATIC EXPRESSIONS AND EQUATIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - QUADRATIC EXPRESSIONS AND EQUATIONS EXERCISE - Chapter Test
50 Videos
Similar Questions
If n is a positive integer then the probability that 3n has 3 at unit place is
View SolutionThere are n letters and n addressed envelopes . If the letters are placed in the envelopes at random , what is the probability that all the letters are not placed in the right evelope ?
View SolutionFor how many positive integral values of n does n! end with precisely 25 zeros?
View SolutionThe smallest positive integral value of n for which (1+√3i)n2 is real is
View SolutionWrite the least positive integral value of n for which (1+i1−i)n is real.
View SolutionWrite the least positive integral value of n for which (1+i1−i)n is real.
View SolutionWrite the least positive integral value of n for which (1+i1−i)n is real.
View SolutionThe probability of a random variable X is given below
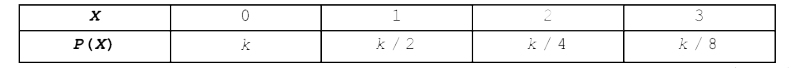
Determine the value of k
View SolutionThe least integral value of x for which 33−x(2+3x)>0 is
View SolutionA random variable 'X' has the following probability distribution :

The values of k is
View Solution
