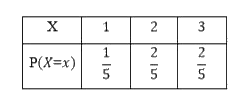Let X~B(n,p) then the mean or expected value of r. v. X is denoted by E(X) and is given by μ=E(X)=npq. True or False
The correct Answer is:False
To determine whether the statement "Let X~B(n,p) then the mean or expected value of r.v. X is denoted by E(X) and is given by μ=E(X)=npq" is true or false, we need to analyze the definitions and formulas related to the binomial distribution.
1. Understanding the Binomial Distribution:
- The binomial distribution is defined by two parameters: n (the number of trials) and p (the probability of success on each trial). The random variable X follows a binomial distribution, denoted as X∼B(n,p).
2. Expected Value of a Binomial Distribution:
- The expected value (mean) of a binomially distributed random variable X is given by the formula:
E(X)=np
- This means that the mean of X is directly proportional to the number of trials n and the probability of success p.
3. Understanding q:
- In the context of the binomial distribution, q is defined as the probability of failure, which can be expressed as:
q=1−p
- Therefore, the product pq can be interpreted as p(1−p).
4. Variance of a Binomial Distribution:
- The variance of a binomially distributed random variable X is given by:
Var(X)=npq
- This indicates that while the variance involves pq, the expected value does not.
5. Conclusion:
- The statement in question claims that the mean E(X) is equal to npq. However, as established, the mean is actually np and not npq.
- Therefore, the statement is False.
Final Answer:
False
- The binomial distribution is defined by two parameters: n (the number of trials) and p (the probability of success on each trial). The random variable X follows a binomial distribution, denoted as X∼B(n,p).
- The expected value (mean) of a binomially distributed random variable X is given by the formula:
E(X)=np
- This means that the mean of X is directly proportional to the number of trials n and the probability of success p.
- In the context of the binomial distribution, q is defined as the probability of failure, which can be expressed as:
q=1−p
- Therefore, the product pq can be interpreted as p(1−p).
- The variance of a binomially distributed random variable X is given by:
Var(X)=npq
- This indicates that while the variance involves pq, the expected value does not.
- The statement in question claims that the mean E(X) is equal to npq. However, as established, the mean is actually np and not npq.
- Therefore, the statement is False.
False
Topper's Solved these Questions
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Part II PROBABILITY DISTRIBUTIONS (Solve the following)
17 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Part II PROBABILITY DISTRIBUTIONS (ACTIVITIES)
5 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Part II PROBABILITY DISTRIBUTIONS (II. Fill in the blanks)
7 Videos
- PROBABILITY DISTRIBUTIONBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY DISTRIBUTIONEXERCISE - MULTIPLE CHOICE QUESTIONS
9 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - MULTIPLE CHOICE QUESTIONS
8 Videos
Similar Questions
Knowledge Check
Given X ~ B( n, p) if p =0.6 E(X) =6, then the value of Var (X) is
A2.4B2.6C2.5D2.3For X~B (n,p) and E (X) = 12, Var (X) = 4, then the value of n is
A3B48C18D36Let X~B (n, p ), if E (X) = 5, Var (X) = 2.5, then P(X<1) is
A(12)11B(12)10C(12)6D(12)9
Let f(x) be a polynomial in x. They the derivative of f(ex) is given by :
View SolutionGiven X~B(n,p).If E(X)=6 and Var (X) = 4.2, find the value of n.
View SolutionLet X ~ B (n,P). I f E(X) = 5 and Var (x) = 2.5 find n and p
View SolutionGiven X~B(n,p) if E(X) = 6, Var (X) = 4.2 , find the value of n and p.
View SolutionFor X~B (n,p), n = 10, E (X) = 5, then p =
View Solution