Let X denote the sum of the numbers obtained when two fair dice are rolled. Find the variance and standard deviation of X.
The correct Answer is:N/a
Let X repesents the sum of the numbers obtained when two unbiased dice are thrown. Since the sum of two numbers obtained cannot be equal to 1 when two unbiased dice are thrown. Therefore, the values of X can be 2,3,4,5,6,7,8,9,10,11,12.
P(X=2)=P[{1,1}]=136
P(X=3)=P[{(1,2),(2,1)}]=236
P(X=4)=P[{(1,3),(2,2),(3,1)}]=336
P(X=5)=P[{(1,4),(2,3),(3,2),(4,1)}]=436
P(X=6)=P[{(1,5),(2,4),(3,3),(4,2),(5,1)}]
=536
P(X=7)=P[{(1,6),(2,5),(3,4),(4,3),(5,2),(6,1)}]
=636
P(X=8)=P[{(2,6),(3,5),(4,4),(5,3),(6,2)}]
=536
P(X=9)=P[{(3,6),(4,5),(5,4),(6,3)}]=436
P(X=10)=P[{(4,6),(5,5),(6,4)}]=336
P(X=11)=P[{(5,6),(6,5)}]=236
P(X=12)=P[66]=136
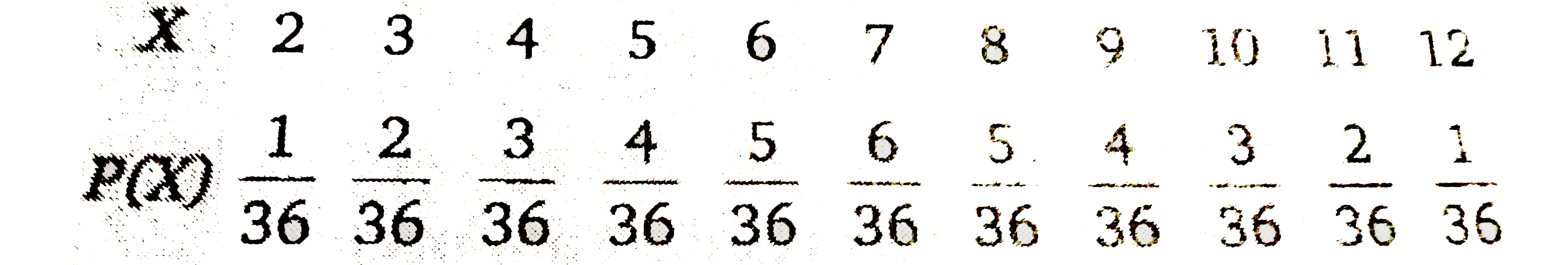
Mean of random variable X
=∑XP(x)
=[2×1+3×2+4×3+5×+6×5+7×6+8×5+9×4+10×3+11×2+12×1]36
=[2+6+12+20+30+42+40+36+30+22+12]36=25236=7
Variance of random variable X=∑X2P(X)−(mean)2
=[22×1+32×2+42×3+52×4+62×5+72×6+82×5+92×4+102×3+112×2+122×1]36−72
=[4+18+48+100+180+294+320+324+300+242+144]36
=197436−49=1974−176436=21036=356
Therefoe, standard deviation,
SD=√variance=√356=√5.833=2.415
Topper's Solved these Questions
- PROBABIILITYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABIILITYEXERCISE - Exercise 13.5
15 Videos
- PROBABIILITYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABIILITYEXERCISE - Miscellaneous Exercise
19 Videos
- PROBABIILITYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABIILITYEXERCISE - Exercise 13.3
14 Videos
- MATRICESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - MATRICESEXERCISE - Miscellaneous Exerice
15 Videos
- RELATIONS AND FUNCTIONS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Miscellaneous Exercise
19 Videos
Similar Questions
If X is the sum of the number when two dice are rolled , then mean variance are
View SolutionFind the variance and standard deviation of the following data:

View SolutionFind the variance and standard deviation from the following data:

View SolutionThere are 4 cards numbered 1,3,5 and 7, one number on one card. Two cards are drawn at random without replacement. Let X denote the sum of the numbers on the two drawn cards. Find the mean and variance of X.
View SolutionThere are 5 cards numbered 1 to 5 , one number on one card . Two cards are drawn at random without replacement . Let X denotes the sum of the numbers on two cards drawn . Find the mean and variance of X.
View SolutionFind the variance and standard deviation of the following distribution

View SolutionFind the mean variance and standard deviation using short-cut method

View SolutionFind the mean, variance and standard deviation using short-cut method.
View SolutionTwo numbers are selected at random (without replacement) from positive integers 2,3,4,5,6, and 7 . Let X denote the larger of the two numbers obtained. Find the mean and variance of the probability distribution of X .
View SolutionTwo numbers are selected are random (without replacement) from positive integers 2, 3, 4, 5, 6 and 7. Let X denote the larger of the two numbers obtained. Find the mean and variance of the probability distribution of X.
View Solution
