Let x2−(m−3)x+m=0(mεR) be a quadratic equation . Find the values of m for which the roots are real and distinct Solution in Punjabi
Let f(x)=x2−(m−3)x+m
Here a=1,b=−(m−3),c=m
and D=b2−4ac=(m−3)2−4m
=m2−10m+9=(m−1)(m−9)
and x-x coordinate of vertex =−b2a=(m−3)2
(i) Both the roots are smaller than 2 D≥0
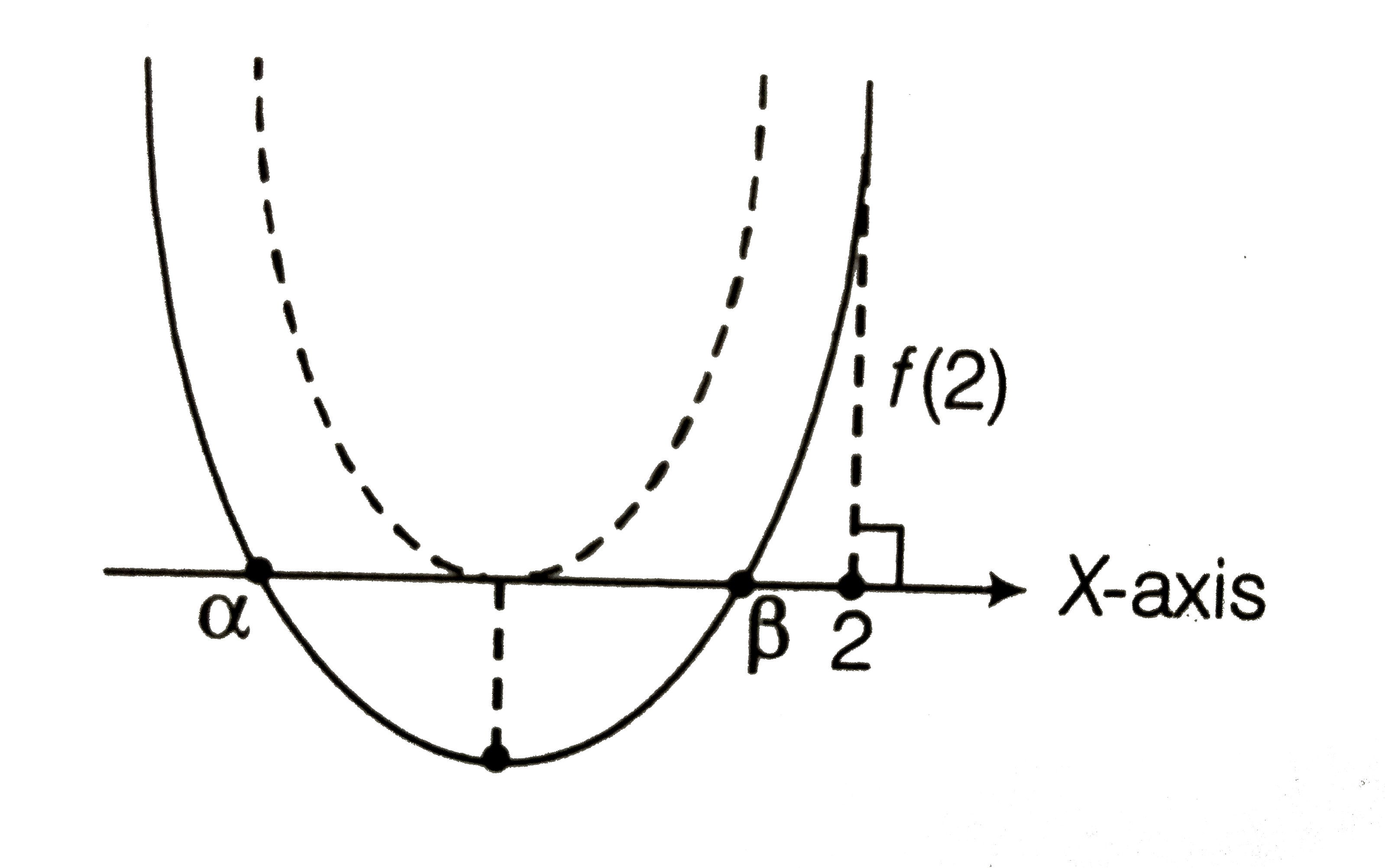
i.e. (m−1)(m−9)≥0
∴mε(−∞1[∪[9,∞) ............i
f(2)>0
i.e. 4−2(m−3)+m≥0
⇒m<10
∴mε(−∞,10)......ii and x- coordinate of vertex <2
i.e. (m−3)2<⇒m<7
∴mε(−∞,7) iii
On combining Eqs.i,ii, and iii we get
mε(−∞,1]
(ii) Both the roots are greater than 2 D≥0
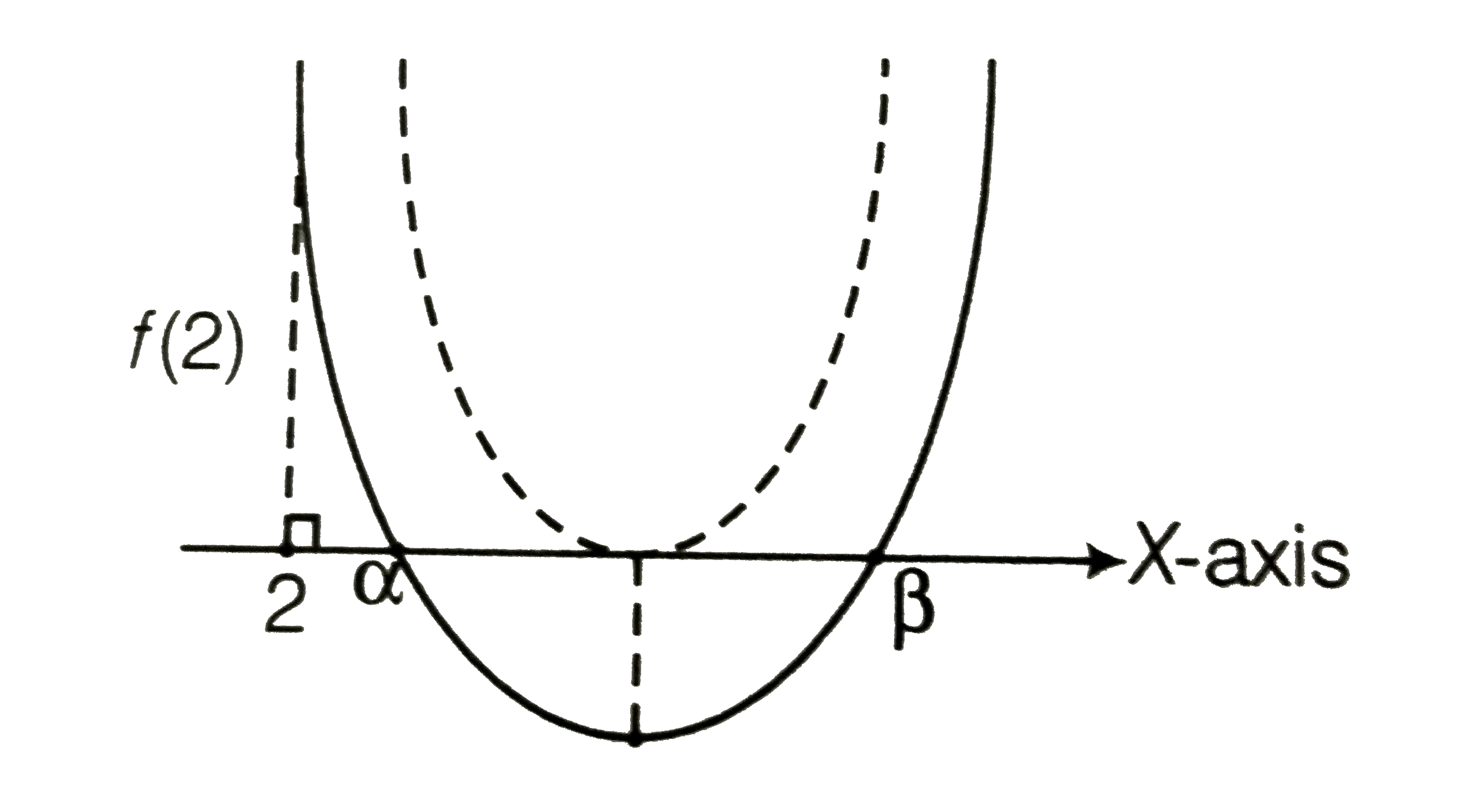
i.e. (m−1)(m−9)≥0
∴mε(−∞,1]ε[9,∞).........i
f(2)>0
i.e. 4−2(m−3)+m>0
⇒m<10......ii
and x-coordinate of vertex >2
i.e. (m−3)2>⇒m<7
∴mε(7,∞) .....iii
On combining Eqs. i, ii and iii we get
mε[9,10)
(iii) One root is smaller than 2 and the other root is greater than 2
D<0
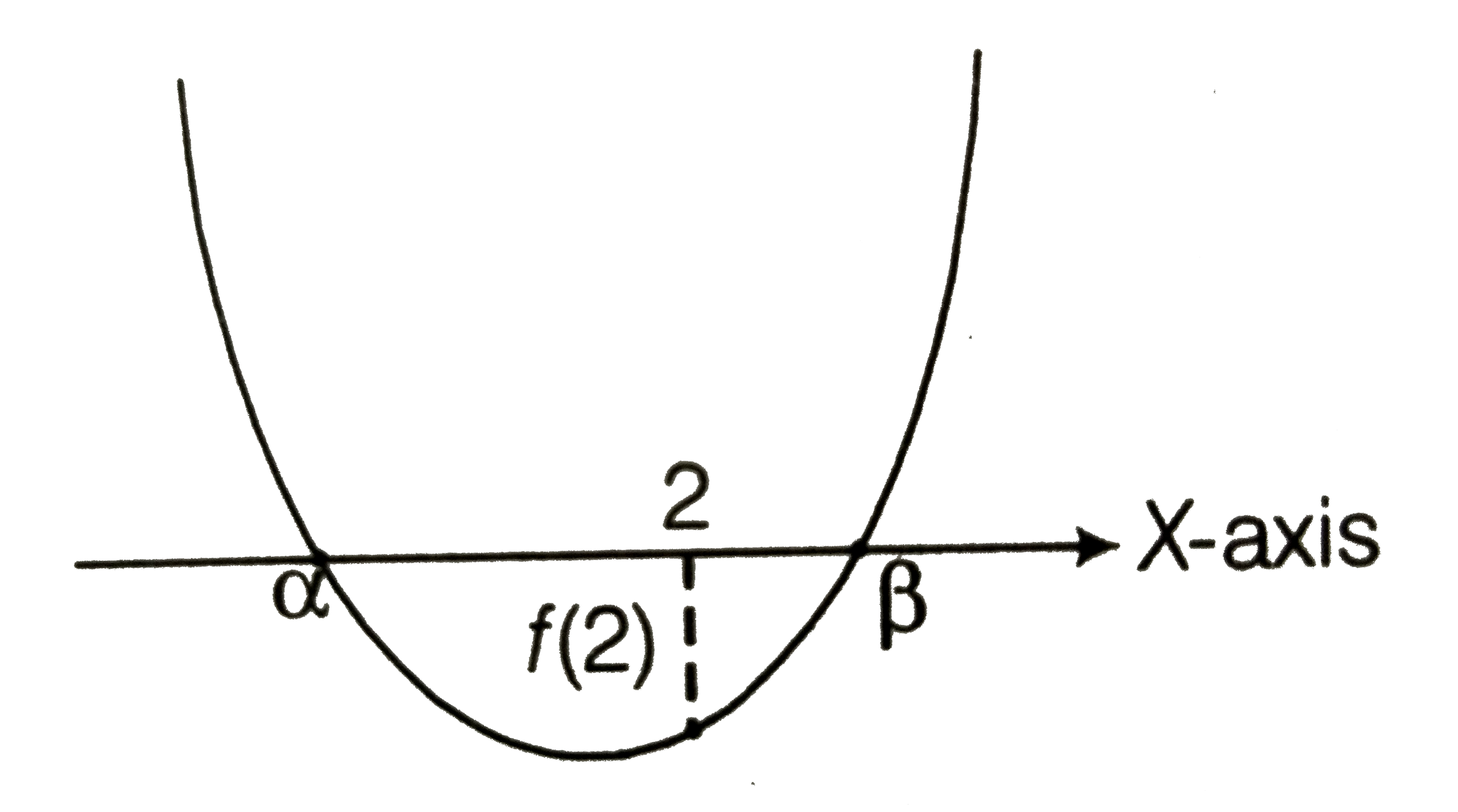
i.e. (m−1)(m−9)>0
∴mε(−∞,1)∪(9,∞)....i
f(2)<0
i.e 4−2(m−3)+m<0
∴m>10
∴mε(10,∞)....ii
On combining Eqs i and ii we get
mε(10,∞)
(iv) Exactly one root lies in the interval (1,2)
D>0
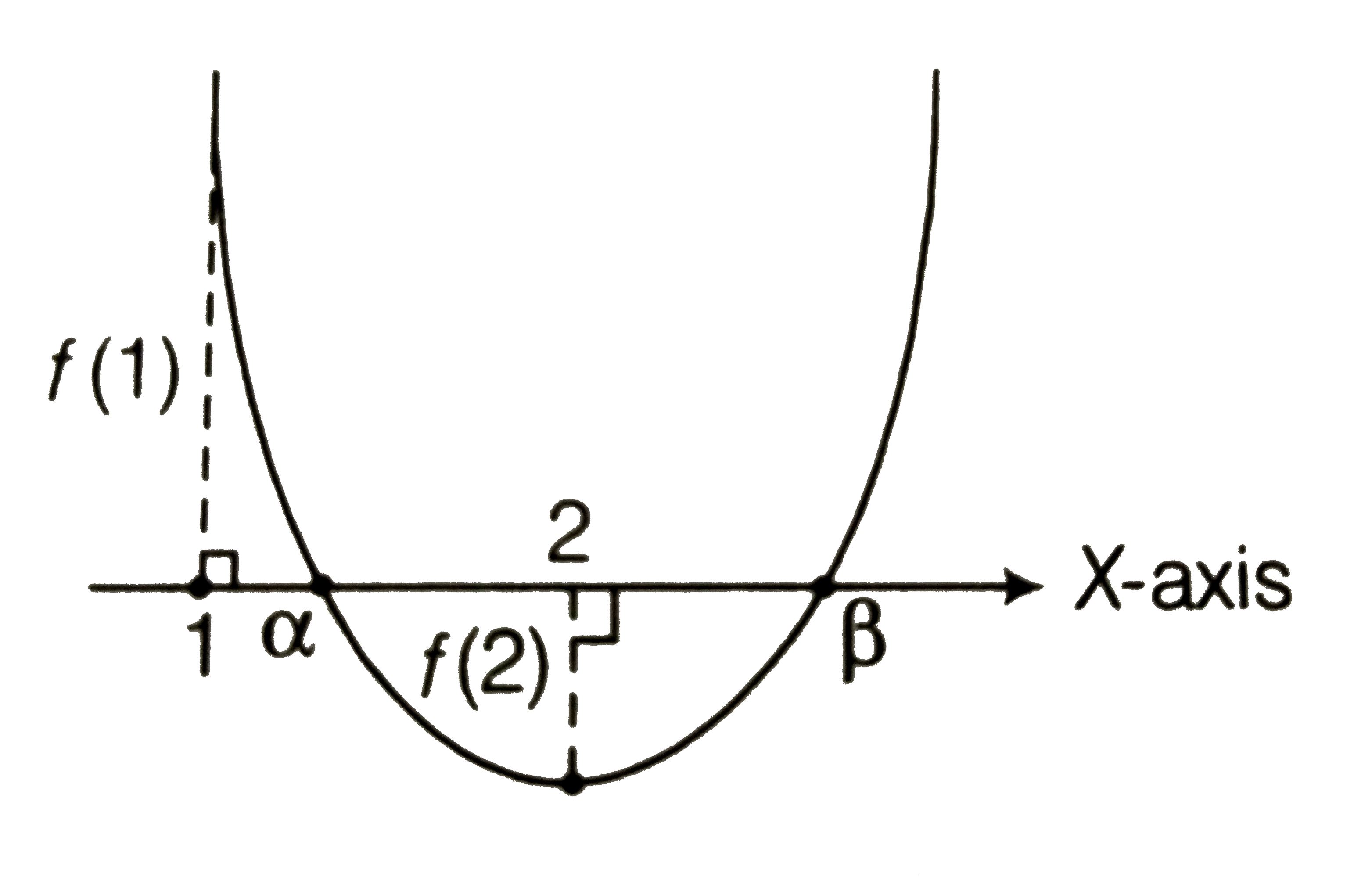
i.e., (m−1)(m−9)>0
∴mε(−∞,1)∪(9,∞)...i
f(1)f(2)<0
(1−(m−3)+m)(4−2(m−3)+m)<0
⇒4(−m+10)<0
⇒m−10>0⇒m>10
∴mε(10,∞) ....ii
On combining Eqs (i) and (ii) we get
mε(10,∞)
(v) Both the roots lie in the interval (1,2)
D≥0
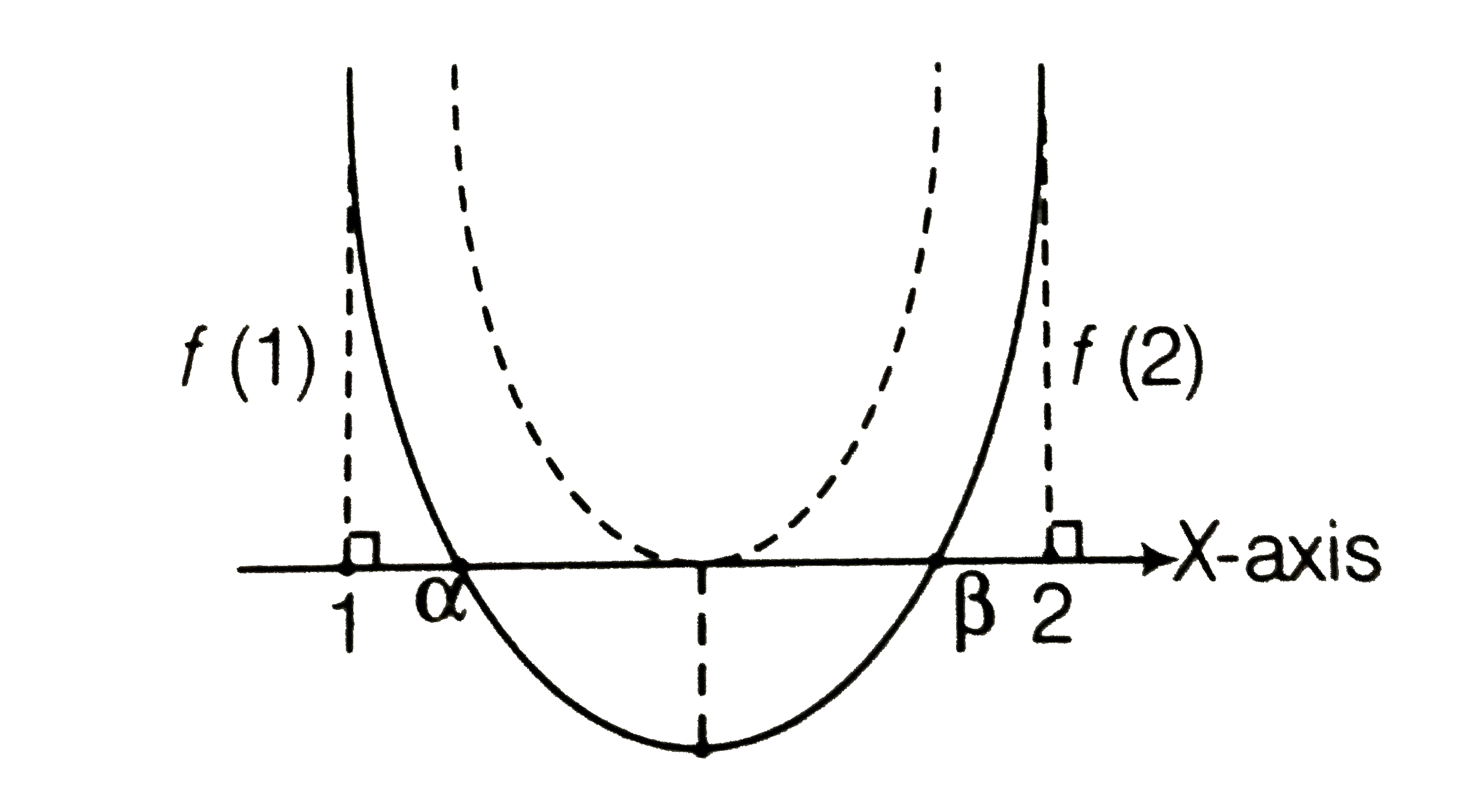
i.e. (m−1)(m−9)≥0
∴mε(−∞,1]∪[9,∞)...i
f(1)>0
i.e. (1−(m−3)+m)>0⇒4>0
∴mεR.ii
f(2)>0
i.e. 4−2(m−3)+m>0⇒m<10
∴mε(−∞,10)..iii
1<x coordinate of vertex <2
i.e. 1<(m−3)2<2
⇒2<m−3<4 or 5<m<7
∴mε(5,7).iv
On combining Eqs. i,ii,iii and iv we get
mεϕ
(vi) One root is greater than 2 and the other root is smaller than 1D>0
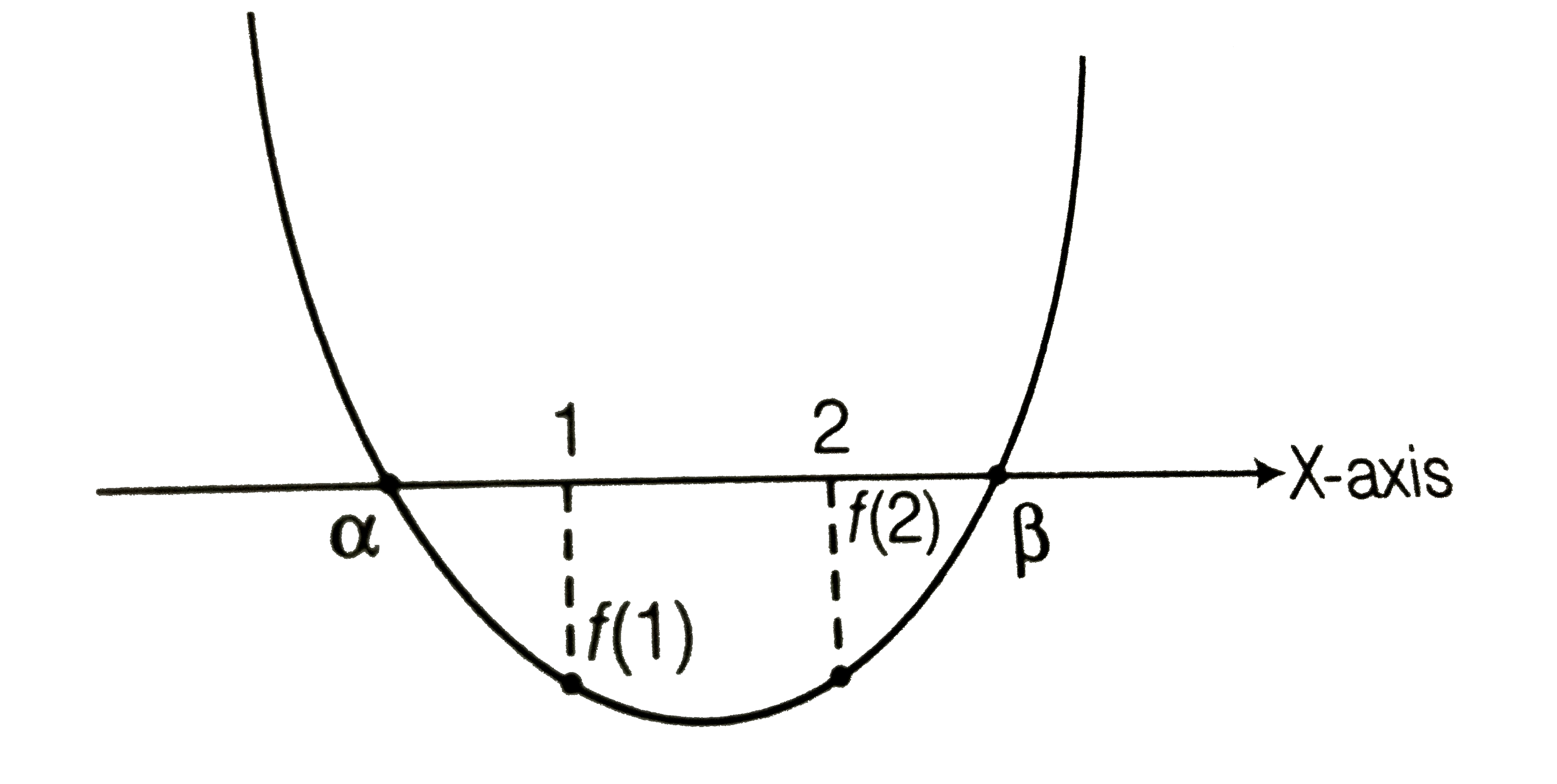
i.e. (m−1)(m−9)>0
∴mε(−∞,1)∪(9,∞).i
f(1)<0
i.e. 4<0 which is not possible.
Thus , no such m exists.
(vii) At least one root lie in the interval (1,2)
Case I Exactly one root lies in (1,2)
mε(10,∞) [from (iv) part]
Case II Both roots lie in the interval (1,2).
mε(10,∞)
(viii) Atleast one root is greater than 2
Case I One root is smaller than 2 and the other root is greater than 2.
Then, mε(10,∞) [from iii) part]
Case II Both the roots are greaters than 2 then mε[9,10).
Hence atleast one root is greater than 2.
∴mε(10,∞)∪[9,10) or mε[9,10)∪(10,∞)
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise For Session 1
11 Videos
- THEORY OF EQUATIONSBOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise For Session 2
10 Videos
- THE STRAIGHT LINESBOOK - ARIHANT MATHSCHAPTER - THE STRAIGHT LINESEXERCISE - The Straight Lines Exercise 8 : (Questions Asked in Previous 13 years Exams)
1 Videos
- THREE DIMENSIONAL COORDINATE SYSTEMBOOK - ARIHANT MATHSCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Three Dimensional Coordinate System Exercise 12 : Question Asked in Previous Years Exam
2 Videos
Similar Questions
If (a2−1)x2+(a−1)x+a2−4a+3=0 is identity in x , then find the value of a .
View SolutionIf α and β are the roots of the equation 2x2−3x+4=0, then the equation whose roots are α2 and β2, is a. 4x2+7x+16=0 b. 4x2+7x+6=0 c. 4x2+7x+1=0 d. 4x2−7x+16=0
View SolutionSolve the following system of inequalities graphically
x+5y≤25,2x+2y≥2,2x−2y≤0,x≥0,y≥0
View SolutionConsider the line L1:x−12=y−1=z+31,L2:x−41=y+31=z+32 find the angle between them.
View SolutionLet x^(2)-(m-3)x+m=0(m in R) be a a quadratic equation.Find the value of m for which the roots
View SolutionLet x2−(m−3)x+m=0(m∈ R) be a quadratic equation. Find the value of m for which the roots are
(i) real and distinct
(ii) equal
(iii) not real
View SolutionFind the values of 'm' for which the equation x4−(m−3)x2+m=0 has
No real roots
View Solution( m - 12 )x^(2) + 2( m- 12 )x + 2 = 0 If the roots of this quadratic equation are real and equal then find the value of m.
View SolutionLet x2−(m−3)x+m=0(mεR) be a quadratic equation . Find the values of m for which the roots are real and distinct
View SolutionLet x2−(m−3)x+m=0,(m∈R) be a quadratic equation. Find
the values of m for which the roots are real and distinct
View SolutionLet x2−(m−3)x+m=0,(m∈R) be a quadratic equation.
Find the values of m for which the roots are equal
View SolutionLet x2−(m−3)x+m=0,(m∈R) be a quadratic equation. Find
the values of m for which the roots are not real
View SolutionLet x2−(m−3)x+m=0,(m∈R) be a quadratic equation. Find
the values of m for which the roots are opposite is sign
View SolutionLet x2−(m−3)x+m=0,(m∈R) be a quadratic equation. Find
the values of m for which the roots are positive
View SolutionLet x2−(m−3)x+m=0,(m∈R) be a quadratic equation. Find
the values of m for which the roots are negative
View SolutionLet x2−(m−3)x+m=0,(m∈R) be a quadratic equation. Find
the values of m for which the roots are positive
View Solution
